Нахождение (вычисление) энергетического спектра эргодического СС по амплитудному спектру его реализации.

Пусть 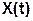– стационарный эргодический СС с нулевым математическим ожиданием .

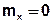Известна одна достаточно протяженная реализация 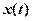. Вырежем кусок этой реализации протяженностью 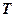и назовем этот кусок усеченной реализацией.

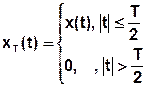
Напомним, что реализация 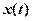и усеченная реализация 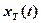– детерминированные сигналы.

Найдем спектральную характеристику усеченной реализации .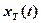

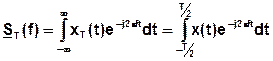
Найдем энергию усеченной реализации, выделяемую на единичном сопротивлении, считая, что СС электрического происхождения.

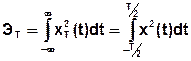(1)

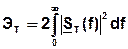(2)

Приравняем (1) и (2), разделим обе части на 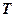и возьмем предел при :

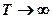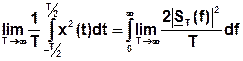
Так как левая часть равенства равна 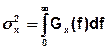, то

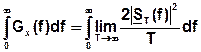
Отсюда:

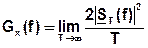(3)

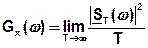(4)

Вывод: чтобы найти энергетический спектр эргодического СС, нужно вычислить амплитудный спектр его усеченной реализации 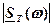возвести в квадрат и разделить на длительность реализации 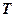, при условии, что 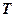достаточно велика.

Классификация СС.

По своим свойствам все СС можно разбить на несколько групп:

1) СС бывают:

- непрерывные,

- импульсные;

- аналоговые,

- дискретные.

2)

- нестационарные,

- стационарные,

- эргодические.

3)По закону распределения:

- нормальные (гауссовские),

- негауссовские.

4) По ширине спектра:

- широкополосные,

- узкополосные.

§9. Гауссовский (нормальный) СС.

СС 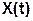называется нормальным, если любые его мгновенные значения 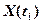есть нормальные СВ.

СВ 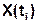– одномерная СВ – называется нормальной, если она распределена по закону Гаусса.

Обозначим 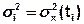– дисперсия в сечении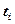

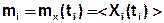─ математическое ожидание в сечении ;

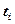Гауссовский закон распределения

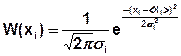
Для удобства обычно используют нормированный гауссовский закон распределения.

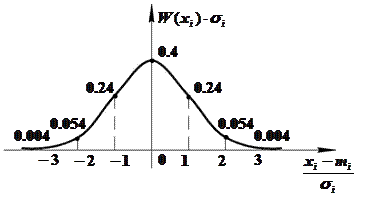
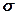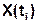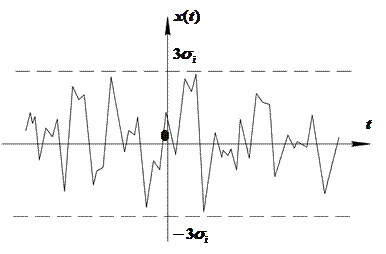
Учитывая, что для гауссовского СС справедливо правило трёх : вероятность превышения СВ значения 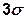ничтожно мала, изобразим примерный вид реализации гауссовского случайного сигнала:

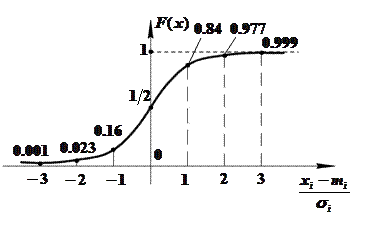
Интегральный закон распределения гауссовской СВ