Узкополосный СС. Закон распределения его огибающей и фазы.
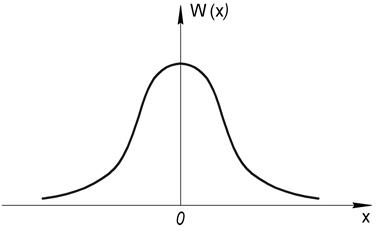
СС Х(t) – называется узкополосным, если его энергетический спектр сосредоточен в основном вблизи некоторой центральной частоты f0 и ширина этого спектра много меньше частоты f0.
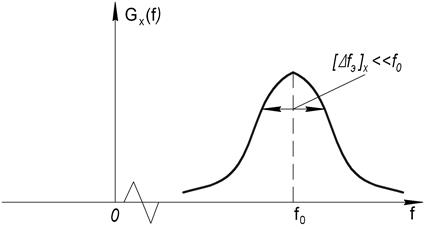
Пусть Х(t) – стационарный гауссовский узкополосный СС с нулевым математическим ожиданием mx=0 и дисперсией 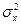 .
.
Запишем выражение для СС по аналогии с радиосигналом.
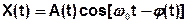
Где А(t) – случайная огибающая,
φ(t) – случайная фаза.
Найдем закон распределения огибающей W(A) и закон распределения фазы W(φ).
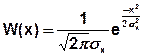
Воспользуемся разложением cos(α-β)=cosαcosβ+sinαsinβ.
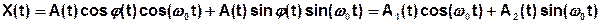
В учебниках доказывается, что новые (вспомогательные) СС А1(t) и А2(t) являются стационарными нормальными СС с математическим ожиданием mА1= mА2=0 и дисперсией 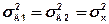
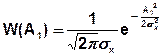
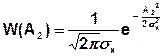
Если выразить А1 и А2 через А и φ.
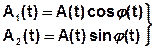 - ортогональные СС
- ортогональные СС
Из высшей математики известно, что ортогональные СС всегда статистически независимы.
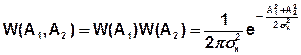
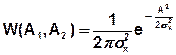
Проведем замену переменных (А1, А2) на (А, φ).
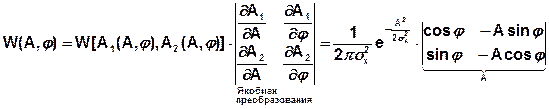
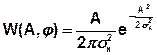
Зная двумерную плотность найдем одномерную:
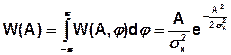
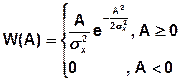 - Релеевский закон распределения
- Релеевский закон распределения
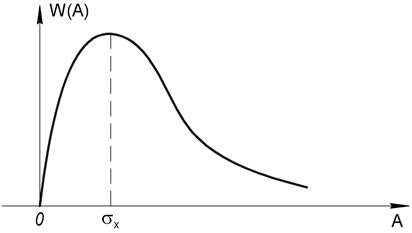
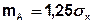
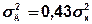
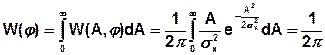
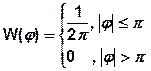 - равномерный закон распределения
- равномерный закон распределения
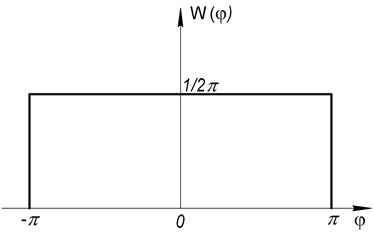
Оказывается W(A, φ)=W(A) W(φ), т. е. огибающая и фаза СС статистически независимы.
Линейная фильтрация СС (прохождение СС через линейную РЭЦ).
Дата добавления: 2021-04-21; просмотров: 604;











