Сопротивление контура при резонансе

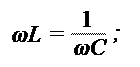Резонанс в параллельном колебательном контуре наблюдается при равенстве реактивных сопротивлений индуктивной и емкостной ветвей:

В этом случае ток I в неразветвленной части цепи совпадает по фазе с входным напряжением U (рис. 1.9, b). При резонансе наблюдается резкое увеличение токов I_L и I_C в параллельных ветвях контура, в то время, как общий ток I в неразветвленной части цепи остается незначительным. Поэтому параллельный резонанс называется резонансом токов.

При резонансе ток I в неразветвленной части контура равен:

I = ;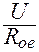

где U – напряжение на входе контура;

R_ое – эквивалентное сопротивление параллельного колебательного контура при резонансе.

Резонансный ток I_кв контуре, образованном параллельными ветвями, протекает одновременно как через индуктивность, так и через емкость:

	Iк = IL = IC ;

Токи в индуктивной и емкостной ветвях:

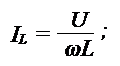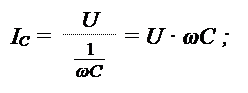Мощность, подводимая к контуру, равна мощности, выделяемой на активном сопротивлении контура:

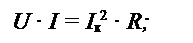
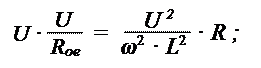Разделив обе части уравнения на U ², получаем:

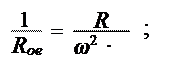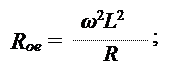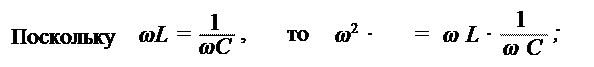
Тогда эквивалентное сопротивление контура при резонансе можно выразить следующим образом:

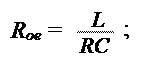Выразим R_ое через добротность контура:

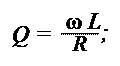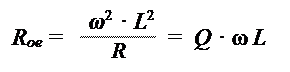Таким образом, эквивалентное сопротивление R_ое параллельного колебательного контура при резонансе в Q раз больше, чем реактивное сопротивление каждой из ветвей контура. Практически величина R_ое составляет несколько десятков кОм.

Полоса пропускания

Любой колебательный контур обладает свойством избирательности. Чем меньше разность Δf между частотой f источника сигнала и резонансной частотой f₀ контура, тем больший ток создает в контуре этот источник.

Полоса частот 2Δf, в пределах которой ток в контуре превышает уровень, составляющий 1/ 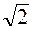» 0,7 от максимального, называется полосой пропускания контура. Ширина полосы пропускания контура зависит от его резонансной частоты и добротности:

Чем ниже добротность контура, тем шире его полоса пропускания при одной и той же резонансной частоте. Это свойство иногда используется для расширения полосы пропускания колебательного контура: с целью уменьшения добротности в цепь контура специально вводят резистор, увеличивающий активное сопротивление контура.

На рис. 3.1.10 показаны границы относительной полосы пропускания двух контуров, имеющих разную добротность.

Рис. 3.1.10. Обобщенные резонансные кривые колебательных контуров