Выражение для индуктивности сложных контуров. Индуктивности участков.
При определении собственных и взаимных индуктивностей контуров, состоящих из нескольких участков, двойной интеграл по нитям i’ и i” в формуле (7) для 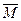 можно представить в виде двойной суммы таких же интегралов по длинам отдельных участков, после чего для собственной индуктивности L контура, состоящего из n-участков, и взаимной индуктивности М двух контуров, состоящих из n и m участков, получим
можно представить в виде двойной суммы таких же интегралов по длинам отдельных участков, после чего для собственной индуктивности L контура, состоящего из n-участков, и взаимной индуктивности М двух контуров, состоящих из n и m участков, получим
L = 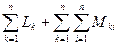 , i
, i 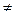 k; (8)
k; (8)
M = 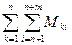 , (9)
, (9)
где Lk и Mki – интегралы вида (5) и (6), соответствующие отдельным участкам контуров. Эти величины, широко используемые при расчете индуктивностей контуров сложной формы, будем называть соответственно собственной индуктивностью k-го участка и взаимной индуктивностью k-го и i-го участков.
При постоянном токе и низкой частоте они могут быть определены по формулам:
Lk = 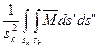 ; (10)
; (10)
Mki = 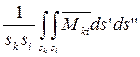 ; (11)
; (11)
А при весьма высокой частоте по формулам:
Lk = 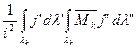 ; (12)
; (12)
Mki = 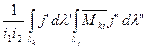 , (13)
, (13)
где
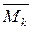 =
= 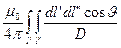 . (14)
. (14)
Здесь 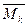 - взаимная индуктивность двух нитей тока i’ и i”, проходящих через элементы ds’ и ds” площади s или соответственно через элементы dλ’ и dλ” периметра λ поперечного сечения k-го участка;
- взаимная индуктивность двух нитей тока i’ и i”, проходящих через элементы ds’ и ds” площади s или соответственно через элементы dλ’ и dλ” периметра λ поперечного сечения k-го участка; 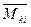 - то же для нитей, проходящих через элементы площадей sk и si или соответственно периметров λk и λi поперечных сечений k-го и i-го участков; j’ = di’/dλ’ и j” = di”/dλ” – линейные плотности тока в точках расположения элементов dλ’ и dλ”; D и
- то же для нитей, проходящих через элементы площадей sk и si или соответственно периметров λk и λi поперечных сечений k-го и i-го участков; j’ = di’/dλ’ и j” = di”/dλ” – линейные плотности тока в точках расположения элементов dλ’ и dλ”; D и 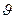 - расстояние и угол между элементами длины dl’ и dl” нитей l’и l”. Интегрирование по нитям l’и l” производится лишь в пределах соответствующих участков.
- расстояние и угол между элементами длины dl’ и dl” нитей l’и l”. Интегрирование по нитям l’и l” производится лишь в пределах соответствующих участков.
Общие формулы в 4.2.1 и 4.2.2. являются основными при расчете индуктивностей. Однако в большинстве случаев для получения необходимых формул приходится делать ряд дополнительных допущений и пренебрежений, основанных, в частности на малости размеров по сравнению с другими.
Метод участков.
Метод участков, применяемый при расчете индуктивностей контуров, состоит в том, что контур или контуры сложной формы разбивают на отдельные участки, каждый из которых имеет сравнительно простую форму, после чего определение индуктивностей сложных контуров сводится с помощью формул (8) и (9) к определению индуктивностей отдельных участков. Особенно отчетливо преимущество метода участков проявляются в случае, когда контуры состоят из прямолинейных участков.
В этом случае для определения собственной индуктивности какого-нибудь контура достаточно иметь только общее выражение индуктивности прямолинейного провода и общее выражение взаимной индуктивности двух таких проводов при произвольном взаимном их расположении в пространстве, а для определения взаимной индуктивности двух контуров достаточно только последнего из упомянутых выражений. Оба выражения могут быть получены, и, следовательно, в рассматриваемом случае расчет индуктивностей может быть сведен к шаблонному применению формул (8) и(9).
Дата добавления: 2021-02-19; просмотров: 636;











