Уравнения состояния газа

Рассмотрим четыре процесса сжатия - изотермный, адиабатный, политропный и изобарный, наблюдаемые в идеальном компрессоре, в котором про­цесс всасывания газа и выталкивания его из цилиндра после окончания процесса сжатия протекает при р = const.

В основу описаний конкретных процессов сжатия газов положено уравне­ние состояния идеального газа Клапейрона:

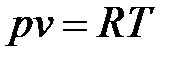
, (9.28)

где р, v, Т - давление, удельный объем и температура сжимаемого газа; R - газовая постоянная.

Уравнение (9.28) с точностью, достаточной для анализа, можно применить для описания параметров процесса сжатия при давлениях не свыше 10 МН/м², т. е. наиболее распространенных в практике нефтедобычи и нефтехимии.

Изотермный процесс сжатия газов характеризуется постоянством температуры в процессе, для которого Т = const, и, следовательно, dT = 0.

В этом случае уравнение (9.28) имеет вид

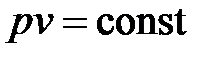, (9.34)

т. е. отвечает закону Бойля - Мариотта.

Линии 1 - 2 процесса, соответствующие изотермному сжатию газов в коор­динатах р - v и Т- s, приведены на рис. 9.2, а, б.

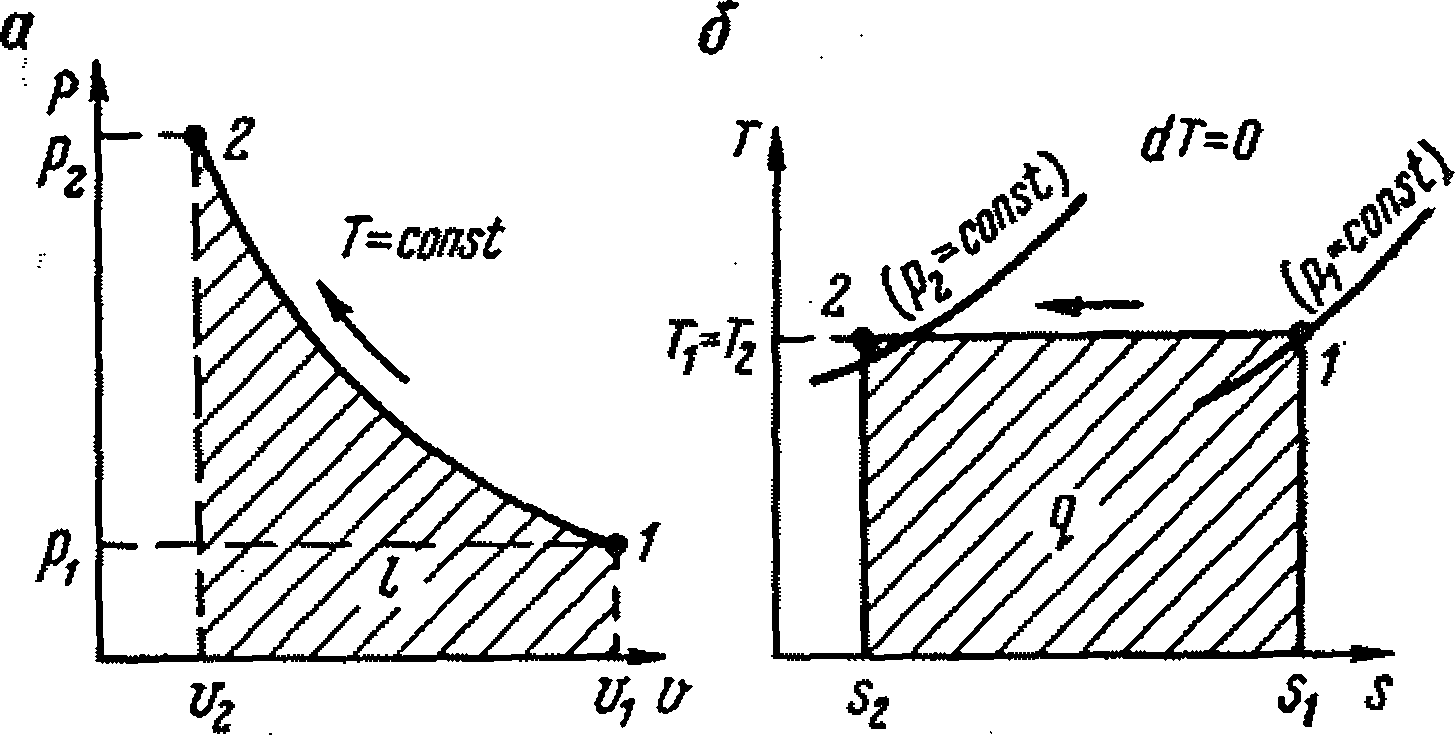
а - в координатах р - v; б - в координатах Т- а

Рисунок - 9.2 Изотермный про­цесс сжатия газа

Адиабатным называется процесс сжатия газов, который протекает в теплоизолированной системе. В этом процессе отсутствует отвод тепла, выделя­ющегося при сжатии газов, т. е.

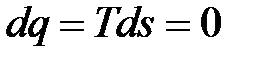
(9.38)

Поскольку энтропия процесса ds = dq/T_, то при адиабатном процессе сжатия газов ds = 0, т. е. s = const, т. е. вся механическая энергия сжатия затрачивается на приращение внутрен­ней энергии.

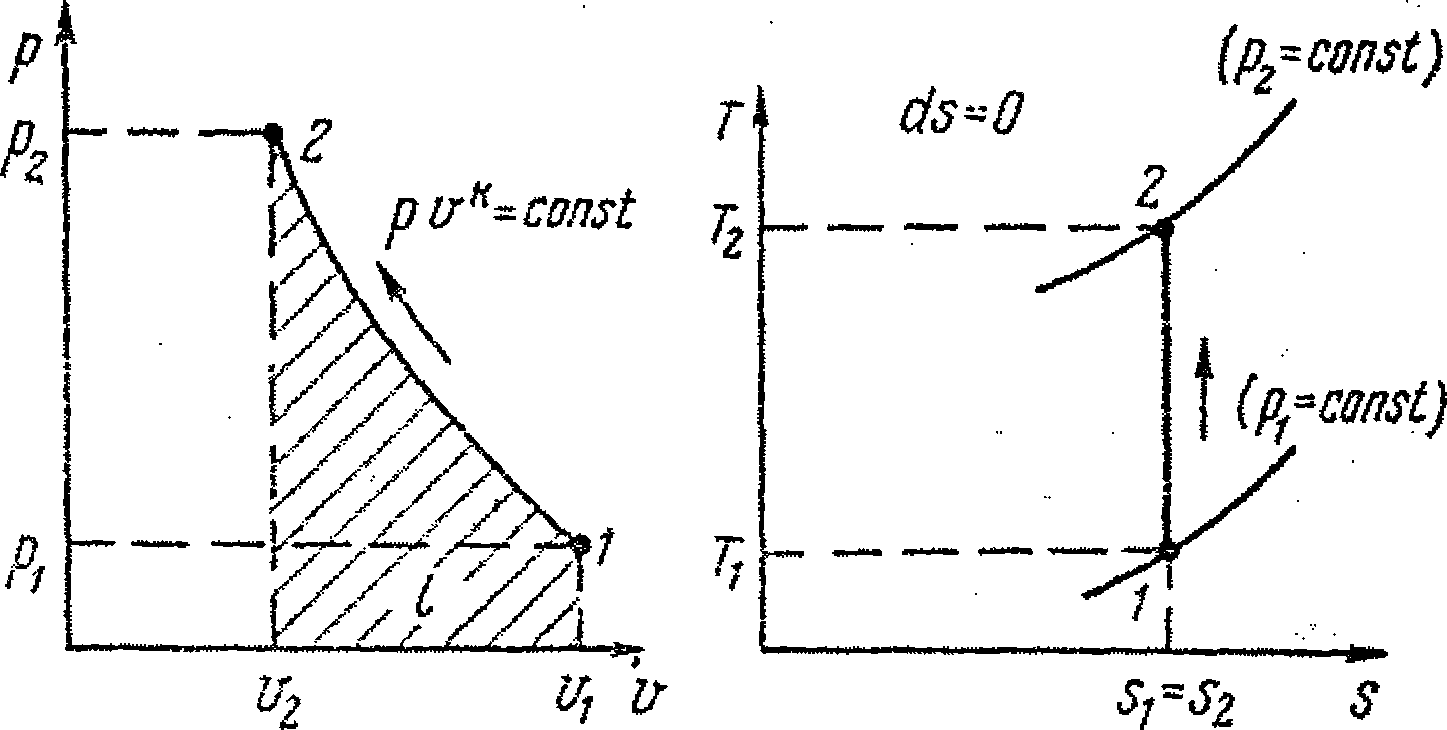
а - в координатах р - v; б - в координатах Т - s

Рисунок - 9.3 Адиабатный про­цесс сжатия газа

Линии 1-2 адиабатного процесса сжатия газа в координатах р-v и Т-s приведены на рис. 9.3, а, б.

Ранее было указано, что термическая работа (выделенное тепло)

dq = Td=0,

а величина к = c_p/c_v называется показателем адиабаты.

Реальные процессы при работе компрессоров не являются адиабатными, так как в процессе сжатия имеется теплообмен, т. е. dq 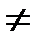0. Однако степень охлаждения не такая, чтобы осуществлялось изотермное сжатие, т. е. dТ 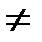0.

Подобные процессы сжатия газов называются политропными.

По аналогии с адиабатным процессом уравнение состояния политропного процесса

pvⁿ = const (9.48)

является уравнением политропы, в котором число п называется показателем политропы.

Таким образом, чтобы найти показатель политропы, надо определить р и v для каких-либо двух точек процесса.

Политропный процесс сжатия газа (рис. 9.4, а, б) может быть осуществим как с отводом тепла (процесс компримирования в обычных компрессорах).

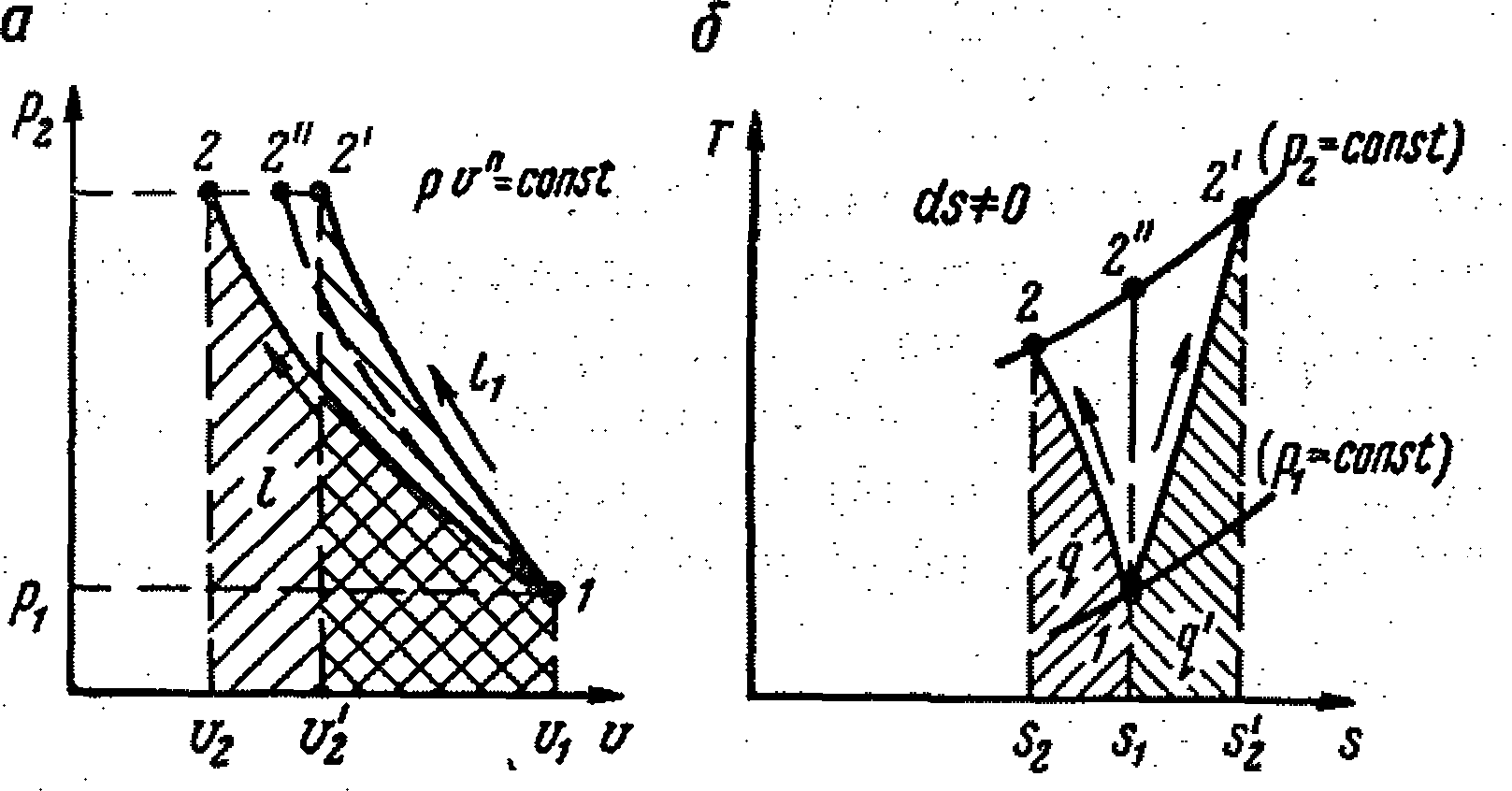
а - в координатах p-v;

б - в координатах Т-s; 1-2 - при п < к; 1-2' - при п = к

Рисунок 9.4 - Политропный процесс сжатия газа

при п < к, так и с подводом тепла (работа холодильных компрессоров на некоторых режимах) при п > к.

Как видно из рис. 9.4, политропный процесс сжатия газа при п < к приводит к уменьшению энтропии (q < 0), а при п > к - к росту энтропии (q > 0).

В идеальном компрессоре процесс заполнения цилиндра компрессора газом, а также вытеснение из цилиндра газа после окончания процесса сжатия должен производиться при постоянных давлениях р₁ и р₂.

Если рассмотреть уравнение состояния (9.28), то изобарный процесс будет соответствовать закону Гей-Люссака:

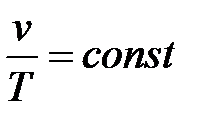(9.52)

так как R/p = const.

На рис. 9.5, а, б в координатах р - v и Т - s проведена линия изобарного процесса.

Как видно из рис. 9.5, работа, затрачиваемая на сжатие газа,

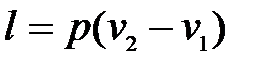(9.53)

Собственно сжатия как такового, т. е. повышения давления газа, в этом случае нет. Есть просто процесс вытеснения газа, т. е. приведение объема 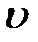₂

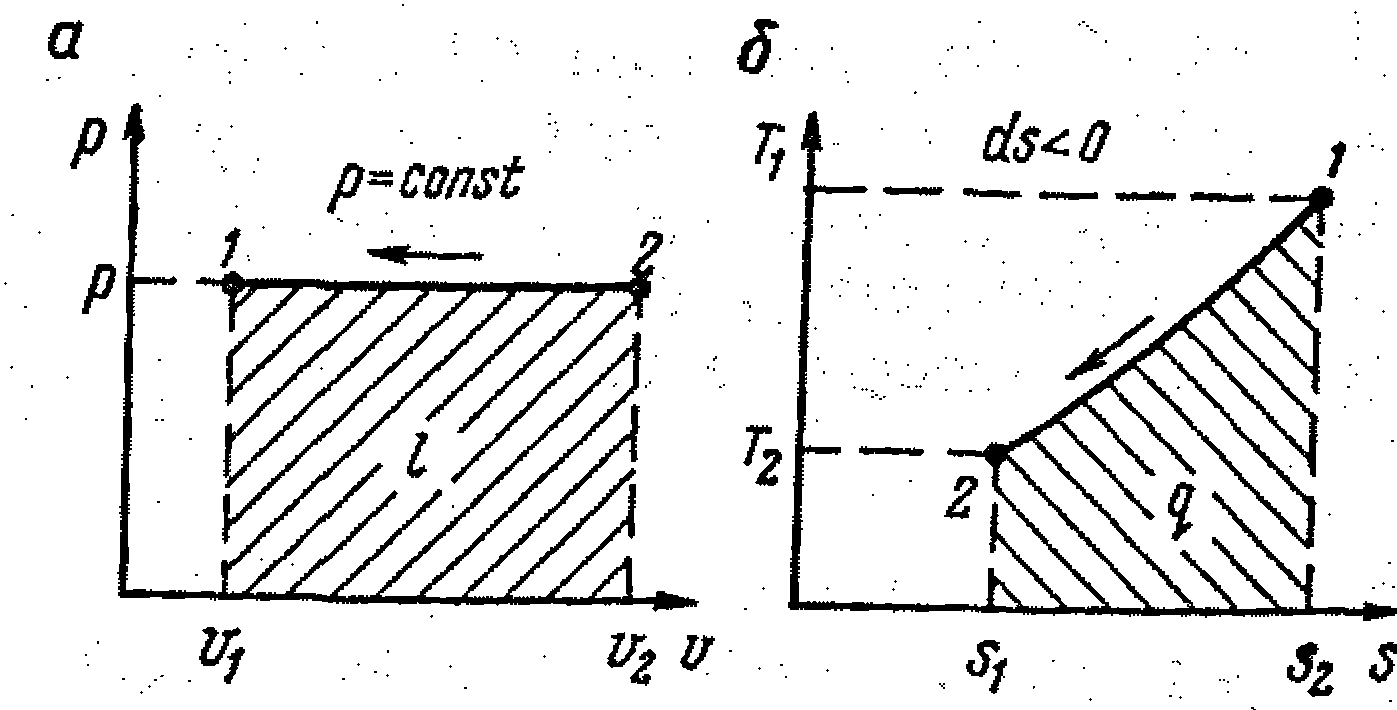
а - в координатах p-v; б - в ко­ординатах Т-s

Рисунок - 9.5. Изобарный процесс сжатия газа

к объему 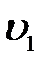при постоянном давлении. Процесс идет в этом случае в сторону уменьшения энтропии системы.

Величина уменьшения энтропии, аналогично (9.51), равна:

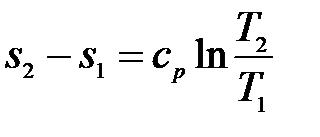(9.54),

где с_р - средняя изобарная теплоемкость за время процесса. При этом количество тепла

.

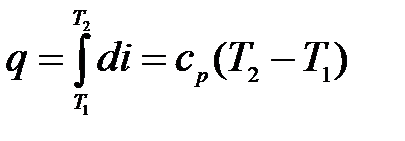Таким образом, если за общее уравнение состояния принять уравнение политропного процесса (9.48), то уравнения рассмотренных выше процессов будут являться его частными случаями: при n = к для адиабатного процесса; при n = 1 для изотермного процесса; при п = 0 для изобарного процесса.

Компрессоры проектируются и выпускаются с определёнными показателями (характеристиками) работы, которые должны удовлетворять условиям их применения.

К ним относятся: производительность компрессора Q в м³/с; развиваемый напор (давление) р в Н/м²; потребляемая мощность N в кВт; коэффициент полезного действия 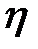в %; степень сжатия 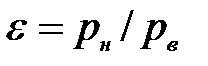; температура комприми­рования t в °С.