Лекция 4. Плоскопараллельное движение твердого тела
План лекции:
1. Плоскопараллельное движение твердого тела.
2. Мгновенный центр скоростей.
3. Свойства плоскопараллельного движения.
Плоскопараллельным (или плоским) называется такое движение твердого тела, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости.
Уравнения xA = f1(t); yA = f2(t); γ = f3(t), определяющие закон происходящего движения, называются уравнениями плоскопараллельного движения твердого тела (рис. 25).
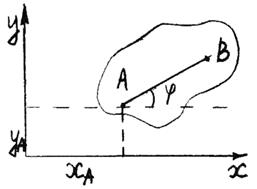
Рис. 25
Плоскопараллельное движение твердого тела слагается из поступательного движения, при котором все точки тела движутся так же, как полюс A, и из вращательного движения вокруг этого полюса.
Основными кинематическими характеристиками рассматриваемого движения являются скорость и ускорение поступательного движения, равные скорости и ускорению полюса vпост. = vA , а = aA, а также угловая скорость ω и угловое ускорение ε вращательного движения вокруг полюса.
Скорость любой точки М геометрически складывается из скорости какой-нибудь другой точки А, принятой за полюс, и скорости точки М в ее вращении вместе с телом вокруг этого полюса. Модуль и направление скорости vM находятся построением соответствующего параллелограмма (рис. 26)
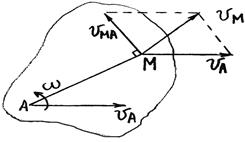
Рис. 26
Проекции скоростей двух точек твердого тела на прямую, соединяющую эти точки, равны друг другу (рис. 27).

Рис. 27
vB cosβ = vA cosα
Мгновенным центром скоростей называется точка сечения S тела, скорость которой в данный момент времени равна нулю (рис. 20).
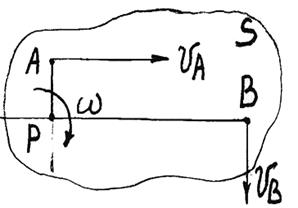
Рис. 20
Скорость любой точки тела, лежащей в сечении S, равна ее вращательной скорости вокруг мгновенного центра скоростей Р.
vA = ω ∙ PA (vA ^ PA)
vB = ω ∙ PB (vB ^ PB)
Скорости точек тела пропорциональны их расстояниям до мгновенного центра скоростей:
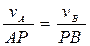
Свойства плоскопараллельного движения
1. Для определения мгновенного центра скоростей надо знать только направления скоростей vA и vB каких-нибудь двух точек А и В сечения тела; мгновенный центр скоростей находится в точке пересечения перпендикуляров, восстановленных из точек А и В к скоростям этих точек (или к касательным к траекториям).
2. Для определения скорости любой точки тела надо знать модуль и направление скорости какой-либо одной точки А тела и направление скорости другой его точки В.
3. Угловая скорость тела равна в каждый момент времени отношению скорости какой-либо точки сечения S к ее расстоянию от мгновенного центра Р.
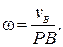
Частные случаи определения мгновенного центра скоростей
1.Если плоскопараллельное движение осуществляется путем качения без скольжения одного цилиндрического тела по поверхности другого, причем второе тело неподвижно, то точка касания Р (рис. 21а) имеет в данный момент времени скорость, равную нулю, и, следовательно, является мгновенным центром скоростей (vp = 0).
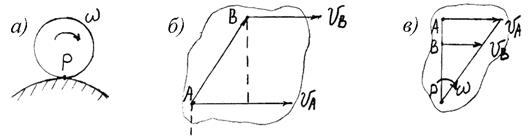
Рис. 21
2. Если скорости точек А и В тела параллельны друг другу, причем линия АВ не перпендикулярна к vA (рис. 21б), то мгновенный центр скоростей лежит в бесконечности и скорости всех точек параллельны vA. Следовательно, скорости всех точек тела в данный момент времени равны друг другу и по модулю и по направлению, т. е. тело имеет мгновенное поступательное распределение скоростей (такое состояние движения тела называют мгновенно поступательным). Угловая скорость тела в этот момент времени равна нулю.
3. Если скорости точек А и В тела параллельны друг другу и при этом линия АВ перпендикулярна к vA, то мгновенный центр скоростей Р определяется построениями, показанными на рис. 21в. В этом случае, в отличие от предыдущих, для нахождения центра Р надо, кроме направлений, знать еще и модули скоростей vA и vВ.
4. Если известен вектор скорости vВ какой-нибудь точки сечения S и угловая скорость ω, то положение мгновенного центра скоростей Р, лежащего на перпендикуляре к vB (рис. 21), можно найти из равенства
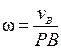 , отсюда
, отсюда 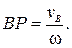
Ускорение любой точки М тела геометрически складывается из ускорения какой-либо другой точки, принятой за полюс, и ускорения точки М в ее вращении вместе с телом вокруг этого полюса. Модуль и направление ускорения aM находятся построением соответствующего параллелограмма (рис. 22).
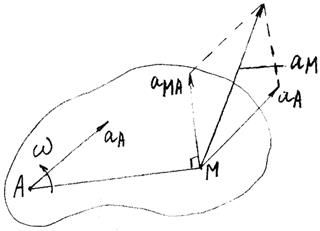
Рис. 22
Вектор 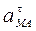 направлен перпендикулярно АМ в сторону вращения, если оно ускоренное, и против вращения, если оно замедленное; вектор
направлен перпендикулярно АМ в сторону вращения, если оно ускоренное, и против вращения, если оно замедленное; вектор 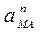 всегда направлен от точки М к полюсу А (рис. 23).
всегда направлен от точки М к полюсу А (рис. 23).
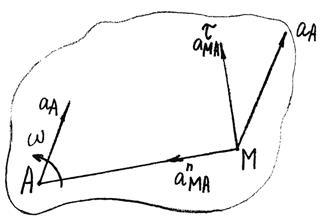
Рис. 23.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Чем характеризуется плоскопараллельное движение твердого тела?
2. Свойства плоскопараллельного движения
3. Сформулируйте теорему о проекциях.
4. Как находится мгновенный центр скоростей?
Лекция 5. Динамика
План лекции:
1 Основные законы и задачи динамики.
2 Силы инерции
3 Работа и мощность.
4 Коэффициент полезного действия (КПД).
5 Внешние и внутренние силы. Метод сечений.
Динамика – это часть теоретической механики, в которой рассматриваются движение материальной точки или тела под действием приложенных сил, а также устанавливается связь между приложенными силами и движениями точек и тел.
Динамика делится на две части: динамика материальной точки и динамика материального тела.
Дата добавления: 2016-10-26; просмотров: 4742;











