Центральное проецирование

Задается плоскость проекций П_о и центр проецирования S, точка А, не лежащая в плоскости.

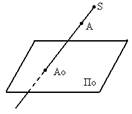Проведем из S через А прямую до пересечения с плоскостью П_о . Получим центральную проекцию А_о точки А.

S – центр или полюс проецирования

П_о - плоскость проекций

SA_о - проецирующий луч (проецирующая прямая)

А_о - центральная проекция точки А на плоскость

1 свойство: при заданных плоскости проекций и центре проецирования одна точка в пространстве имеет одну центральную проекцию.

Но если есть проекция точки, S и П, то точку в пространстве найти нельзя.

2 свойство: каждая точка на плоскости проекций может быть проекцией бесконечного множества точек.

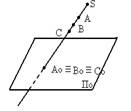
Центральным проецированием может быть построена проекция любой линии или поверхности как множество проекций всех её точек.

Центральные проекции линии не определяют проецируемую линию.

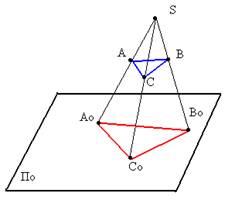
Для построения проекций линий, поверхностей или тел часто достаточно построить проекции лишь некоторых характерных точек.

ПРИМЕР: При построении на П_о проекции ∆ АВС достаточно построить проекции А_о, В_о, С_о трех его точек – вершин А, В и С.

Центральное проецирование применяют для изображения предметов в перспективе, но для технического черчения этот метод неудобен.