Параллельное проецирование

Его можно рассматривать как частный случай центрального, при котором центр проецирования удален в бесконечность.

Применяют параллельные проецирующие прямые, проведенные в заданном направлении.

Если направление проецирования перпендикулярно плоскости проекций, то проецирование называют прямоугольным или ортогональным.

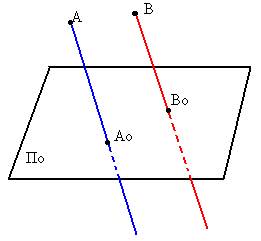
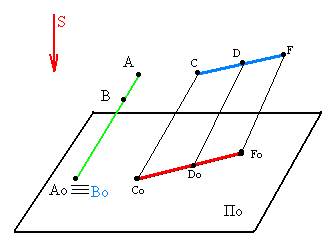
При параллельном проецировании сохраняются все свойства центрального, а так же возникают следующие свойства:

а). Проекции взаимно // прямых //, а отношение длин отрезков таких прямых равно отношению длин их проекций

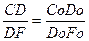
б). Плоская фигура, // плоскости проекций проецируется на эту плоскость в натуральную величину

в). Если прямая перпендикулярна направлению проецирования, то её проекцией является точка

Если есть центр параллельной проекции, мы не сможем определить положение точки в пространстве.

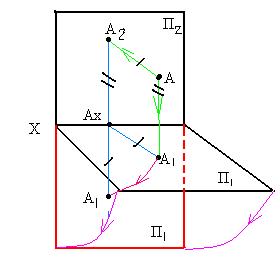Гаспар Монж предложил взять две взаимно перпендикулярные плоскости проекций (горизонтальную П₁ и фронтальную П₂) и используя метод прямоугольного проецирования направить проецирующие лучи перпендикулярно плоскостям.

П₁ – горизонтальная плоскость проекций

П₂ -фронтальная плоскость проекций

X- ось проекций- линия пересечения плоскостей П₁ и П₂ или П₁ /П₂

A_x A₁ и A_x A₂ – перпендикулярны оси X –линии связи

Если есть в пространстве точка А, то опускаем из неё перпендикуляр на П₁ (горизонтальная проекция точки А – А₁) и на плоскость П₂ (фронтальная проекция точки А – А₂)

Но данное наглядное изображение точки в системе П₁/П₂ для целей черчения неудобно.

Преобразуем его так, чтобы горизонтальная плоскость проекций совпала с фронтальной, образуя одну плоскость чертежа.

Это преобразование осуществляется путем поворота вокруг оси Х плоскости П₁ на угол 90^о вниз. При этом A_x A₂ и A_x A₁ образуют один отрезок, расположенный на перпендикуляре к оси проекций Х, называемом линией связи.