Линейные операции над матрицами

Матрицы и определители

Раздел 1. Матрицы

Матрицейназывается множество чисел, образующих прямоугольную таблицу, которая содержит m строк и nстолбцов. Для записи матрицы используется следующее обозначение:

Для любого элемента а_{i j} первый индекс i означает номер строки, а второй индекс j – номер столбца.

Пусть дана таблица (называемая матрицей), состоящая из четырех чисел: .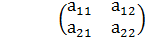

Матрица имеет две строки a₁₁ a₁₂ и a₂₁a₂₂ и два столбца a₁₁ и a₁₂ .

a₂₁ a₂₂

Числа, составляющие эту матрицу, обозначены буквой с двумя индексами. Первый индекс указывает номер строки, а второй- номер столбца, в которых стоит данное число. Например, a₁₂ означает число, стоящее в первой строке и втором столбце; a₂₁- число, стоящее во второй строке и первом столбце. Числа a_11, a_12, a_21, a₂₂ будем называть элементами матрицы.

Матрицу для кратности будем обозначать одной буквой, например:

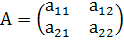, В = .

Две матрицы А и Вназываются равными (А=В), если они имеют одинаковое число строк и одинаковое число столбцов и их соответствующие элементы равны.

Так, есл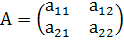и и 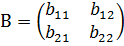, то А=В, если a₁₁= , = , = = .

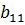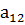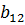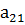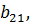
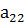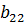Виды матриц:

а) Прямоугольный (Если число строк матрицы не равно числу столбцов (m≠n) например, матрицы А = ,B= ).

Сокращенно прямоугольную матрицу типа m X n можно записал так: А = (а_ij), где i=1, 2, …, m; j = 1, 2, …, n.

б) Квадратный (Если число строк равно числу столбцов (m=n)). Например, А= , B= .

Число строк или столбцов квадратной матрицы называется ее порядком. Так, в последнем примере порядок матрицы А равен 2, а порядок матрицы В равен 4.

Диагональ, содержащую элементы а₁₁, а₂₂, …, а_nn, будем называть главной, а диагональ, содержащую элементы а_1n, а_2,n-1, …, а_n1, - побочной (или вспомогательной).

в) Диагональный (Матрица у которых отличны от нуля только элементы, находящиеся на главной диагонали: А= . Например, матрицы А= 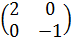, В= ;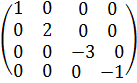

г) Скалярный (Если у диагонали матрицы все числа главной диагонали равны между собой, т.е. а₁₁=а₂₂=…=а_nn ;

д) Единичный (Если в скалярной матрице все числа главной диагонали равны единице и обозначается буквой Е:

Е= ;

е) Нулевой (матрица, все элементы которой равны нулю и обозначаются так:

О= ).

Нуль-матрица при сложении матриц выполняет роль обычного нуля при сложении чисел: А+0=А.

Например: + = .

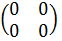В прямоугольной матрице типа m X n возможен случай, когда m=1. При этом получается матрица-строка:

А = (а₁₁ а₁₂ … а_1n).

В случае, когда n = 1, получаем матрицу-столбец:

В = .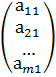

Такие матрицы-строки и матрицы-столбцы иначе будем называть векторами.

ж) Равные (Две матрицы называются равными, если они имеют одинаковое число строк m и одинаковое число столбцов nи их соответствующие элементы равны: а_ij = b_ij).

Так, матрицы

А= 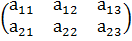и В =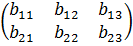

равны, если а₁₁ = b₁₁, а₁₂ = b₁₂, а₁₃ = b₁₃, а₂₁ = b₂₁, а₂₂ = b₂₂, а₂₃ = b₂₃.

Равные матрицы обязательно имеют одно и то же строение: либо обе они прямоугольные типа m X n, либо квадратные одного и того же порядка n.

Если в матрице типаm 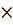n, имеющий вид

А= ,

переставить строки со столбцами, получил матрицу типа n 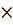m, которую будем называть транспонированной матрицей:

А= .

В том случае, когда матрица состоит из одной строки (матрица-строка), т. е.

В = (b₁ b₂ … b_n),

транспонирования матрица является матрицей-столбцом:

В^т= .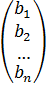

Линейные операции над матрицами

Суммой матриц Аи Вусловимся называть такую матрицу, элементы которой равны сумме соответствующих элементов матриц Аи В. Складывать можно только матрицы, имеющие одинаковые строение: или прямоугольные типа m 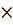n,или квадратные порядка n.

Пусть А = , В =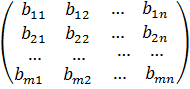

Тогда сумма матриц С= А+В имеет вид

С=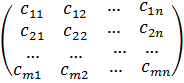

где с₁₁₌a₁₁+b₁₁,c₁₂=a₁₂+b₁₂;……c_ij=a_ij+b_ij,…..,c_mn=a_mn+b_mn.

Если даны две квадратные матрицы одного порядка, например

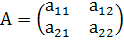и 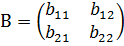, то их суммойназывается матрица

.

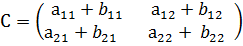Аналогично определяется сумма двух прямоугольных матриц, имеющих одинаковое число строк и одинаковое число столбцов.

Пример 1. + = = .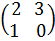

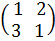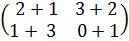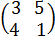Пример 2. + = .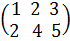

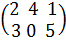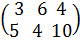Например,сложить матрицы A и B, если:

а) 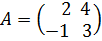, B= .

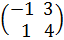Решение.а) Здесь А и В – квадратные матрицы второго порядка. Складывая их соответствующие элементы, получим

С = А + В= = .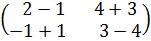

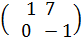б) 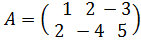, B= .

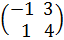Решение.б) Здесь А и В– прямоугольные матрицы типа 2 3. Складываем их: соответствующие элементы

С = А 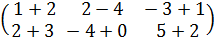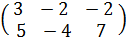+ В= = .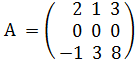

в) , В .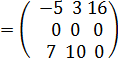

Решение.в) Здесь А и В – квадратные матрицы третьего порядка. Складываем их соответствующие элементы:

С = А + В = = .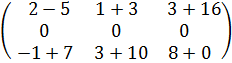

Г) , .

Решение. г) эти прямоугольные матрицы сложить нельзя, так как А есть матрица типа 3Х 2, а В- матрица типа 2Х3; можно складывать прямоугольные матрицы одного типа.

Мы видим, что сложение матриц сводится непосредственно к сложению их элементов, являющихся числами. Поэтому на сложение матриц распространяются важнейшие свойства чисел:

1) переместительный закон сложения: А + В = В + А , где А и В – либо квадратные матрицы одного порядка n, либо прямоугольные матрицы одного типа m X n;

2) сочетательный закон сложения ( А + В ) + С = А + ( В + С ), где А, В, С – либо квадратные матрицы одного порядка n, либо прямоугольные матрацы одного типа m х n.

Например,доказать справедливость равенств:

а) А + В = В + А для матриц

А = , В = ;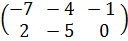

б) (А + В) + С = А + ( В + С ) для матриц

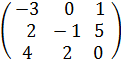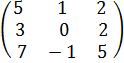А = , В = , С = .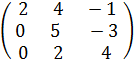

Из сказанного выше вытекает равенство

А + 0 = А,

т.е. существует такая нулевая матрица ( того же порядка или типа) , что ее сумма с матрицей А любого типа равна матрице А.

Для любой матрицы Асуществует матрица - А, такая, что А + (- А) = 0, т.е. матрица, противоположная А.

Произведением матрица Ана число Kназывается такая матрица KА, каждый элемент которой равен 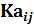, т.е.

если А = , то KА = .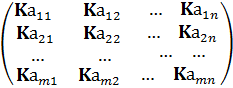

Умножение матрицы на число сводится к умножению на это число всех элементов матрицы.

Например, а) Умножить матрицу А = на число K = 3.

Решение. Умножая каждый элемент матрицы А на 3, получим

3А = .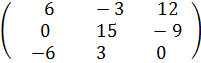

б) Найти матрицу, противоположную матрице А =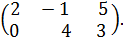

Решение. Для нахождения противоположной матрицы умножаем матрицу

А на K =-1:

- А = .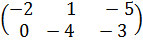

в) Найти линейную комбинацию 3А – 2В, если

А = 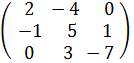, В = .

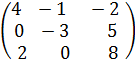Решение: Сначала находим произведение А на K ₁ =3 и Вна K ₂ =-2:

3А = 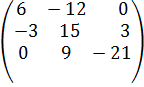, -2В = .

Теперь найдем сумму полученных матриц:

3А – 2В, если А = = .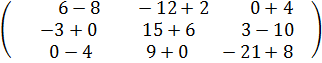

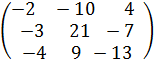Умножение матриц

Рассмотрим умножение квадратных матриц второго порядка.

Пусть

A= , B= .

Произведение этих матриц называется матрица

C=AB= .

Чтобы найти элемент первой строки и первого столбца матрицы С, нужно каждый элемент первой строки матрицы А (т.е. 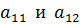) умножить на соответствующий элемент первого столбца матрицы B (т.е. 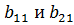) и полученные произведения сложить: ;

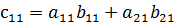чтобы найти элемент с₁₂ первой строки и второго столбца матрицы C, нужно умножить все элементы первой строки (a₁₁ и a₁₂) на соответсвующие элементы второго столбца (b₁₂ и b₂₂)­­ и полученные произведения сложить: c₁₂=a₁₁b₁₂+a₁₂b₂₂;

аналогично находятся элементы c₂₁ и c₂₂.

Вообще, чтобы получить элемент, стоящий на пересечении i-й строки и j-го столбца матрицы-произведения, нужно все элементы i-й строки (a_i1, a_i2,……, a_in) матрицы A умножить на соответсвующие элементы j-го столбца (b_1j, b_2j,…., b_nj) матрицы B и полученные произведения сложить.

Например, а) найти произведение матриц A и B, если

A= 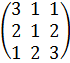, B= ,

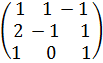Решение. Найдём каждый элемент матрицы-произведения:

c₁₁=a₁₁b₁₁+a₁₂b₂₁+a₁₃b₃₁=3*1+1*2+1*1=6;

c₁₂=a₁₁b₁₂+a₁₂b₂₂+a₁₃b₃₂=3*1+1*(-1) +1*0=2;

c₁₃=a₁₁b₁₃+a₁₂b₂₃+a₁₃b₃₃=3*(-1) +1*1+1*1=-1;

c₂₁=a₂₁b₁₁+a₂₂b₂₁+a₂₃b₃₁=2*1+1*2+2*1=6;

c₂₂=a₂₁b₁₂+a₂₂b₂₂+a₂₃b₃₂=2*1+1*(-1) +2*0=1;

c₂₃=a₂₁b₁₃+a₃₂b₂₃+a₂₃b₃₃=2*(-1) +1*1+2*1=1;

c₃₁=a₃₁b₁₁+a₃₂b₂₁+a₃₃b₃₁=1*1+2*2+3*1=8;

c₃₂=a₃₁b₁₂+a₃₂b₂₂+a₃₃b₃₃=1*1+2*(-1) +3*0=-1;

c₃₃=a₃₁b₁₃+a₃₂b₂₃+a₃₃b₃₃=1*(-1) +2*1+3*1=4;

Следовательно,

С= .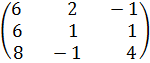

Правило нахождения матрицы-произведения распространяется на умножение прямоугольных матриц.

б) найти произведение AB, если

A= 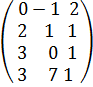, B= .

Решение.

АВ = = .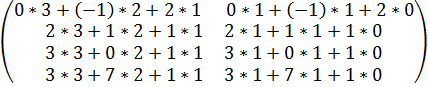

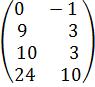Если в этом примере мы попытаемся найти произведение BA, то убедимся, что это невозможно.

Для прямоугольных матриц справедливы следующие правила:

1) умножение матрицы А на матрицу B имеет смысл только в том случае, когда число столбцов матрицы A равно числу строк матрицы B;

2) в результате умножения двух прямоугольных матрицы получается матрица, содержащая столько строк, сколько строк в первой матрице, и столько столбцов, сколько столбцов во второй матрице.