Свойства умножения матриц
Пусть 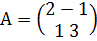 ,
, 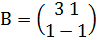 .
.
Найдем произведения AB и BA:
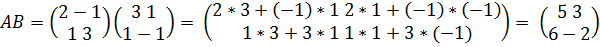
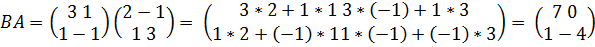
Мы видим, что AB 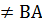 . Этот пример показывает, что произведение двух матриц, вообще говоря, не подчиняется переместительному закону.
. Этот пример показывает, что произведение двух матриц, вообще говоря, не подчиняется переместительному закону.
Можно проверить, что для умножения матриц выполняется сочетательный закон:
A(BC) = (AB)C,
а так же распределительный закон
(A+B)C=AC+BC
Отметим следующий любопытный факт. Известно, что произведение двух отличных от нуля чисел не равно нулю. Для матриц это не всегда справедливо, т.е. возможен случай, когда произведение двух ненулевых матриц может оказаться равным нулевой матрице.
Например, если
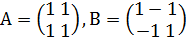 ,
,
то
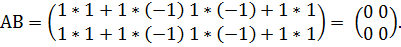
Определитель матрицы.
Определитель матрицы. Вычисление определителей второго и третьего порядков.
Пусть дана квадратная матрица второго порядка
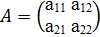
Определителем (или детерминантом) второго порядка, соответствующим данной матрице, называется число а11а22 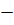 а12а21.
а12а21.
Определитель второго порядка записывается так:
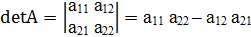
Отметим, что определитель второго порядка равен разности попарных произведений элементов главной и побочной диагоналей.
Например, вычислить определители второго порядка:
a) 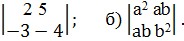
Решение.
а) 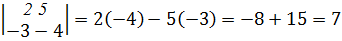
б) 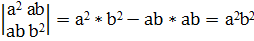 -
- 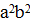 = 0
= 0
Пусть дана квадратная матрица третьего порядка:
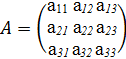
Определителем (или детерминантом) третьего порядка, соответствующим данной матрице, называется число
a11 a21 a33+ a21 a32 a13+ a12 a23 a31 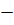 a13 a22 a31
a13 a22 a31 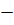 a12 a21 a33
a12 a21 a33 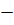 a11 a23 a32.
a11 a23 a32.
Определитель третьего порядка записывается так:
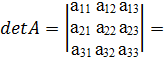
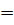 a11 a22 a33+ a21 a32 a13+ a12 a23 a31
a11 a22 a33+ a21 a32 a13+ a12 a23 a31 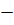 a13 a22 a31
a13 a22 a31 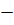 a12 a21 a33
a12 a21 a33 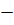 a11 a23 a32.
a11 a23 a32.
При вычислении определителей третьего порядка удобно пользоваться правилом треугольников (правилом Сарруса). Это правило проиллюстрируем на схеме: 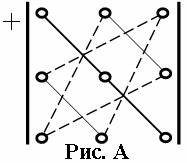
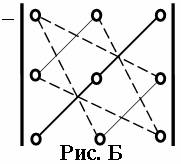
Три положительных члена определителя представляют собой произведения элементов главной диагонали (a11 a22 a33) и элементов, находящихся в вершинах двух равнобедренных треугольников, основания которых параллельны главной диагонали (a12 a23 a31 и a21 a32 a13). Три отрицательных его члена есть произведения элементов побочной диагонали (a13 a22 a31) и элементов, находящихся в вершинах двух равнобедренных треугольников, основания которых параллельны побочной диагонали (a12 a21 a33 и a11 a23 a32).
Например, вычислить определители третьего порядка:
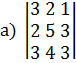 ;
; 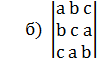 .
.
Решение.
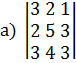 = 3
= 3 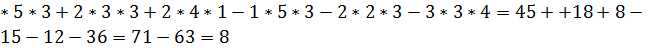
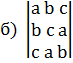 = a·c·b + b·a·c + c·b·a
= a·c·b + b·a·c + c·b·a  c
c 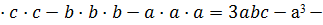
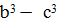
Дата добавления: 2021-04-21; просмотров: 557;











