Миноры и алгебраические дополнения элементов определителя.

Минором M_ij элемента 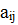определителя D= 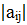, где i и j меняются от 1 до n, называется такой новый определитель, который получается из данного определителя вычеркиванием строки и столбца, содержащих данный элемент.

Например, минор M₁₂, соответствующий элементу 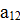определителя

,

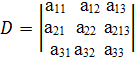Получается, если вычеркнуть из определителя D первую строку и второй столбец, т.е.

.

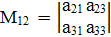Например, а) записать все миноры определителя.

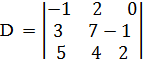
Решение.

;

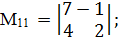
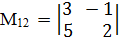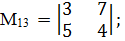
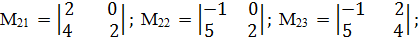
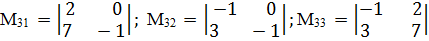
б) записать все миноры определителя

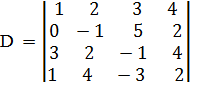
Алгебраическим дополнением элемента a_ij определителя D называется минор M_ij этого элемента, взятый со знаком (-- 1)^i+j. Алгебраическое дополнение элемента a_ij принято обозначать A_ij.

Таким образом, A_ij = (--1) ^i+jM_ij

в) найти алгебраические дополнения элементов a₁₃, a₂₁,a₃₁ определителя

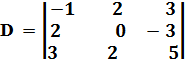
Решение.

A₁₃ = (--1)¹⁺³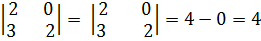

A₂₁ = (--1)²⁺¹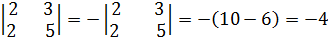

A₃₁ = (--1)³⁺¹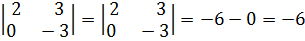

Теорема о разложении определителя по элементам строки или столбца

Сумма произведений элементов любой строки (или столбца) определителя D на их алгебраические дополнения равна этому определителю, т.е.

D = a_i1A_i1+a_i2A_i2+…+a_inA_in

или

D = a_1jA_1j+a_2jA_2j+…+a_njA_nj

Эти соотношения называются разложением определителя, но элементам i-й строки или j-го столбца.

Например, определитель

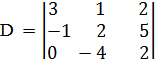
разложить: а) по элементам 1-й строки; б) по элементам 2-го столбца.

Решение.

а)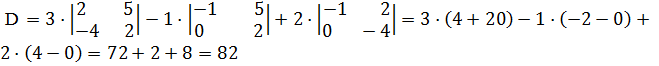

б) .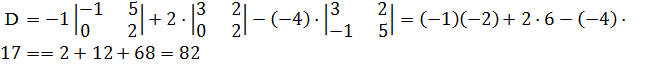

Если определитель имеет четвертый или более высокий порядок, то его также можно разложить по элементам строки или столбца, а затем понижать порядок алгебраических дополнений.

Например, вычислить определитель

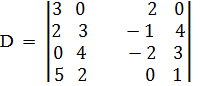
Решение. Разложим определитель по элементам 1-й строки (так как она содержит два нулевых элемента):

· .

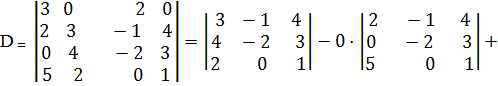
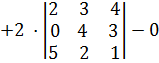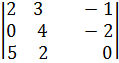Поскольку второй и четвертый члены разложения равны нулю, имеем

.

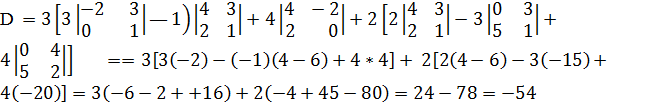Перечислим различные способы вычисления определителей:

1. Определитель можно вычислить, используя непосредственно его определение. Этим способом удобно находить определители второго и третьего порядков, а для определителя более высокого порядка применим следующий способ.

2. Определитель можно вычислить с помощью его разложения по элементам строки или столбца.

3. Определитель можно вычислить способом приведения к треугольному виду. Этот способ основан на том, что в силу свойства 7 треугольный определитель равен произведению элементов главной диагонали.

Чтобы получить треугольный определитель, нужно, используя свойство 6, к какой-либо строке (или столбцу) заданного определителя прибавлять соответствующие элементы другой строки (или столбца), умноженные на одно и то же число, до тех пор, пока не придем к определителю треугольного вида.

Пусть, например, требуется вычислить определитель:

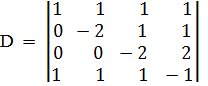
Вычитая первую строку из всех остальных, сразу получим определитель треугольного вида:

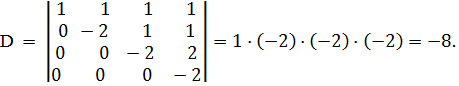
Литература

1. Лисичкин В.Т., Соловейчик И.Л. Математика в задачах с решениями: Учебное пособие. 3-е изд., стер. – СПб.: Издательство «Лань» , 2011, - 464с.: ил. – (Учебники для вузов. Специальная литература).

2.Богомолов Н.В. Практические занятия по математике: Учебное пособие для техникумов.- 3-е изд.- М.: Высшая школа, 1990.-495с.

3.Дадаян А.А. Математика: Учебник 2-е изд.- М.: Форум - Инфра – М, 2006. – 552с.

Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах. В 2-х частях. М.: Оникс 21 веек, 2003.- 303с., 415 с.