Эквивалентное преобразование резистивноготреугольника в звезду.

<6 7 8910 11 12 >

Под соединением треугольником (рис.1.21.а) понимается такое, при котором конец одного элемента соединяется с началом второго, конец второго- с началом третьего, а конец третьего - с началом первого. Узловые точки 1,2,3 подключаются к остальной

Рис 1.21 части электрической цепи. Соединение звездой получается при объединении начал или концов сопротивлений в одну точку (рис.1.21.б).

При расчете электрических цепей оказывается полезно преобразовать треугольник в звезду или совершить преобразование звезды в треугольник.

Замена треугольника эквивалентной звездой должна производиться таким образом, чтобы после указанной замены токи в остальной части цепи, а также напряжения между точками 1 и 2 , 2 и 3,3 и 1 остались без изменения.

С помощью законов Кирхгофа можно получить следующие формулы для определения сопротивлений эквивалентной звезды:

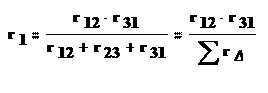
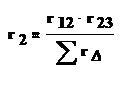
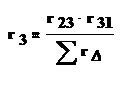( 1.37)

При замене резистивных элементов, соединенных звездой, эквивалентным треугольником, пользуются следующими формулами

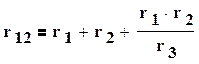
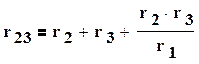(1.38)

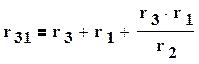
1.8.3. Метод контурных токов.

Метод контурных токов дает возможность упростить расчет электрических цепей по сравнению с методом расчета по законам Кирхгофа за счет уменьшения числа уравнений, которые приходится решать совместно. Этот метод заключается в том, что вместо токов в ветвях определяются на основании второго закона Кирхгофа так Рис 1.22 называемые контурные токи,

замыкающиеся в контурах. На рис.1.22. в виде примера показана двухконтурная цепь, в которой I₁₁ и I₂₂- контурные токи. Токи в сопротивлениях r₁ и r₂равны соответствующим контурным токам; ток в сопротивлении r₃ являющемся общим для обоих контуров, равен разности контурных токов I₁₁ и I₂₂, так как эти токи направлены в ветви r₃встречно.

Число уравнений , записываемых для контурных токов по второму закону Кирхгофа, равно числу независимых контуров, то есть для электрической схемы с числом узлов q и числом ветвей p задача нахождения контурных токов сведется к решению системы p-q +1 уравнений. Так, в схеме рис.1.22 q = 2 p = 3; следовательно, число уравнений равно 3-2+1=2 (число уравнений независимых контуров).

Положительные направления контурных токов задаются произвольно. Направление обхода каждого контура принимается обычно совпадающим с выбранным положительным направлением контурного тока; поэтому при составлении уравнения по второму закону Кирхгофа падение напряжения от заданного контурного тока в сопротивлениях, входящих в контур, берется со знаком плюс. Падение напряжения от тока смежного контура в общем сопротивлении берется со знаком минус, если контурные токи в этом сопротивлении направлены встречно, как это, например, имеет место в схеме рис.1.22., где направление обоих контурных токов выбрано по ходу часовой стрелки.

Для заданной электрической схемы с двумя независимыми контурами (рис.1.22) могут быть записаны два уравнения по второму закону Кирхгофа, а

именно:

, ,

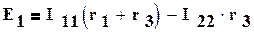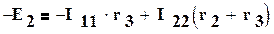здесь (r₁ +r₃) и (r₂ + r₃) - собственные сопротивления контуров 1 и 2, r₃ -

общее сопротивление контуров 1 и 2. После определения контурных токов, легко найти и токи всех ветвей.

I₁ = I₁₁; I₂ = I₂₂ ; I₃ = I₁₁ - I₂₂ .

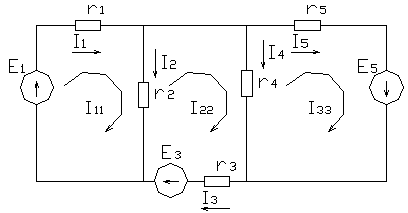
Рис 1.23

Пример 1.2.

Найти токи в схеме (рис. 1.23) при помощи метода контурных токов.

r₁ = r₂ = r₃ = r₄ = r₅ = 10 Ом; E₁ = E₅ = 50 В; E₃ = 90 В.

Решение:

Выбираем направление всех контурных токов I₁₁, I₂₂ , I₃₃ по часовой стрелке.

Записываем систему уравнений:

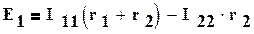
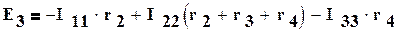
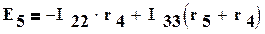
После подстановки численных значений:

,

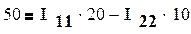
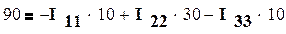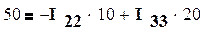
выразим I₁₁ и I₃₃ через I₂₂ :

,

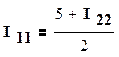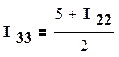
и подставим во второе уравнение системы

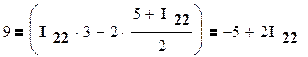
получаем в итоге I₂₂ = 7А ; I₁₁ = I₃₃ = 6А.

В соответствии с выбранным положительным направлением токов в ветвях окончательно получим:

I₁=I₁₁=6A; I₂=I₁₁-I₂₂=6-7= --1A; I₃=I₂₂=6A

I₄=I₂₂-I₃₃=1A; I₅=I₃₃=6A

1.8.4. Метод узловых напряжений.

Метод узловых напряжений заключается в том, что на основании первого закона Кирхгофа определяются напряжения в узлах электрической цепи относительно некоторого базисного узла. Эти искомые напряжения называются узловыми напряжениями, причем положительное направление их указывается стрелкой от рассматриваемого узла к базисному.

Напряжение на какой - либо ветви равно, очевидно, разности узловых напряжений концов данной ветви; произведение же этого напряжения на производимость данной ветви равно току в этой ветви. Таким образом, зная узловые напряжения в электрической цепи, можно найти токи в ветвях.

Если принять потенциал базисного узла равным нулю, то напряжения между остальными узлами и базисным узлом будут равны также потенциалам этих узлов. Поэтому данный метод называется также методом узловых потенциалов.

При наличии одной ветви с э.д.с и бесконечной проводимостью целесообразно принять за базисный узел один из узлов, к которому примыкает данная ветвь, тогда напряжение данного узла становится известным и число неизвестных сокращается на одно.

Число неизвестных в методе узловых напряжений равно числу уравнений, которые надо составить для схемы по первому закону Кирхгофа. Метод узловых напряжений имеет преимущество перед методом контурных токов в том случае, когда число уравнений, записанных по первому закону Кирхгофа, меньше числа уравнений, записанных по второму закону Кирхгофа, или если (q -1) < (p - q + 1 ), или, что то же 2(q-1) <p, где q- число узлов, p -число ветвей.

На рис 1.24 в виде примера изображена электрическая схема, содержащая три узла. Примем потенциал φ₃=0 (базисный узел). Составим уравнения для узлов 1 и 2 по первому закону Кирхгофа:

,

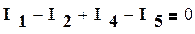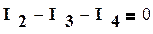(1.39)

Каждые из этих токов можно выразить через узловые потенциалы и э.д.с. ветвей:

;

;

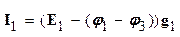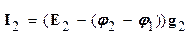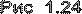
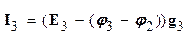; (1.40)

;

.

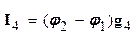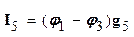Подставив (1.40) в (1.39), сгруппировав члены при φ₁и φ₂ и перенеся члены с э.д.с. в правую часть, получим

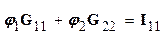
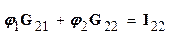(1.41)

где

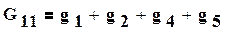
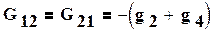
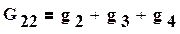(1.42)

.

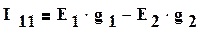
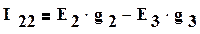Таким образом , множителем при φ₁, является коэффициент G₁₁, равный сумме проводимостей всех ветвей, сходящихся в первом узле (1.42).G₁₂ равняется сумме проводимостей всех ветвей, соединяющих узел 1 с узлом 2, взятой со знаком минус. Ток I₁₁ называют узловым током первого узла. Это расчетная величина, равная алгебраической сумме токов, полученной от деления э.д.с. ветвей, подходящих к узлу 1, на величину сопротивлений этих ветвей. Если э.д.с. направлена к узлу, то берется в I₁₁ со знаком плюс, если от узла, то со знаком минус. Так же определяют G₂₂,G₂₁,I₂₂ (см. 1.42).Если между какими-либо двумя узлами нет ветви, то соответствующая проводимость равна нулю. Решив систему (1.41) относительно φ₁ и φ₂, определим узловые напряжения цепи. Искомые токи определяют либо по закону Ома, либо по второму закону Кирхгофа для участка цепи, содержащей э.д.с.

Частным случаем метода узловых напряжений является метод двух узлов.

При наличии n ветвей между точками a и b применение метода узловых напряжений позволяет ограничиться составлением и решением одного уравнения для определения напряжения Uab между узлами a и b. Задавшись положительным направлением напряжения Uab (см. рис.1.25) и учитывая направления э.д.с в ветвях в соответствии с изложенным выше , получим формулу для определения напряжения Uab:

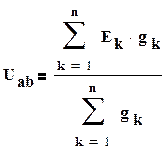(1.43.)

где произведения E_Кg_К берутся со знаком плюс , если э.д.с. действует от узла b к a и со знаком минус при обратном направлении . Токи ветвей определяются по выражению , составленному по второму закону Кирхгофа , при выбранном положительном направлении тока .

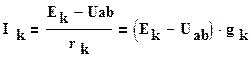(1.44.)

Пользуясь методом двух узлов можно произвести замену искомых параллельных ветвей, содержащих источники э.д.с., одной эквивалентной.

Участок цепи (рис.1.25,а) будет эквивалентен цепи на (рис.1.25,б), если при любых значениях тока I , подтекающего из всей остальной, не показанной на рисунке части схемы, напряжение на зажимах a и b (Uab) в обеих схемах будет одинаковым. Составив уравнения для обеих схем (1.25. а и б) и приравняв

Рис 1.25 коэффициенты при Uab и токи, получим выражения для определения Eэкв и gэкв.

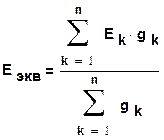(1.45)

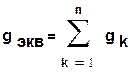(1.46)

.

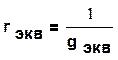При подсчетах по формуле (1.45) следует иметь в виду следующее: если в какой-либо ветви схемы э.д.с. отсутствует, то соответствующее слагаемое в числителе (1.44) выпадает, но проводимость этой ветви в знаменателе (1.45) остается.

Пример 1.3.

В электрической цепи рис. 1.26

E₁=40 B, E₂=20 B, r₀₁=r₀₂=1 Oм, r₁=9 Ом, r₂=39 Ом, r₃=10 Ом,

r₄=30 Ом, r₅=15 Ом, U₁=45 B, U₂=30 B

Пользуясь методом узлового напряжения, определить токи в ветвях.

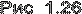Решение.При указанных положительных направлениях напряжения Uаb и токов в ветвях по формуле (1.43) определим Uаb

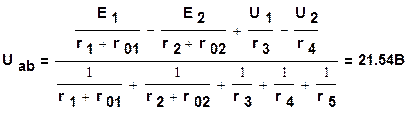
Воспользовавшись формулой (1.44), определим токи в ветвях:

,

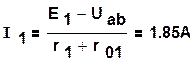
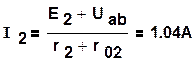
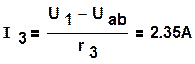
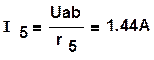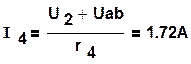
Метод наложения.

При расчете по методу наложения ток в любой ветви электрической цепи определяется как алгебраическая сумма токов, вызываемых в данной ветви каждой из э.д.с. в отдельности, в предположении равенства нулю всех остальных э.д.с.

Порядок расчета цепи методом наложения следующий. Из электрической цепи удаляют все источники э.д.с. и напряжений, кроме одного. Сохранив в электрической цепи все резистивные элементы, в том числе и внутренние сопротивления источников, производят расчет электрической цепи. Подобным образом поступают столько раз, сколько имеется в цепи источников. Результирующий ток каждой ветви определяют как алгебраическую сумму токов от всех источников.

Метод наложения весьма удобен для анализа явлений происходящих в электрических цепях при изменении их параметров.

<6 7 8910 11 12 >

Дата добавления: 2021-04-21; просмотров: 331;