Метод эквивалентного генератора.
Метод эквивалентного генератора используется в случае, когда необходимо найти ток, напряжение или мощность в одной ветви. При этом вся остальная часть цепи, к которой подключена данная ветвь, рассматривается в виде двухполюсника (рис. 1.27, а). Двухполюсник называют активным, если он содержит
Рис 1.27 источники электрической энергии, и пассивным - в противоположном случае. Будем обозначать активный двухполюсник буквой А, а пассивный - буквой П.
Различают две модификации метода эквивалентного генератора: метод эквивалентного источника напряжения и метод эквивалентного источника тока.
Рассмотрим метод эквивалентного источника напряжения. Этот метод базируется на теореме Тевенина, согласно которой ток в любой ветви линейной электрической цепи не изменится, если активный двухполюсник, к которому подключена данная ветвь, заменить эквивалентным источником (генератором) напряжения. Э.д.с. этого источника равна напряжению холостого хода на зажимах разомкнутой ветви, а внутреннее сопротивление равно эквивалентному входному сопротивлению пассивного двухполюсника со стороны разомкнутой ветви (рис. 1.27, б).
Опуская доказательство этой теоремы, после замены активного двухполюсника эквивалентным источником в соответствии с этой схемой имеем:
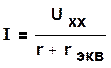 (1.47)
(1.47)
Пример 1.4.
В электрической цепи (рис. 1.28, а).
U=100 B, E= 40 B, r1=r4=30 Ом, r2=r3=20 Ом, r=15 Ом, r0=1 Ом
Пользуясь методом зквивалентного генератора определить I и напряжение Uab.
Рис 1.28
Решение. При отключенном сопротивлении r (рис.1.28б) по закону Ома и на основании второго закона Кирхгофа получим:
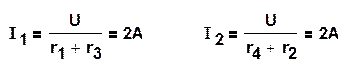
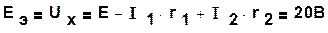
После замены источников их внутренними сопротивлениями получим схему, изображенную на рисунке 1.29в, Между точками аи b последовательно соединены три участка цепи: участок с параллельно соединенными резисторами r1 и r3;участок, на котором параллельно соединены резисторы r2 и r4, и участок, содержащий резистор ro. В соответствии с этим, внутреннее сопротивление эквивалентного генератора (сопротивление относительно точек а и b) будет:
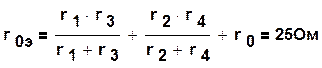
По формуле (1.47) и закону Ома получим
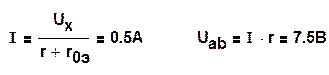
Дата добавления: 2021-04-21; просмотров: 413;











