Математическая модель с логарифмическим «эмиссионным» уравнением для электровакуумного диода.

Здесь можно рассмотреть уже знакомый нам эксперимент С. Дэшмана. Общий вид эмиссионного уравнения:

Для физики процесса х – это напряжение, z – температура, K₁ и K₂ - коэффициенты, регулирующие кривизну участка перехода между процессами.

х и z – аргументы сигналов прямой связи ( аргументы прямой связи ).

x₀ и z₀ – аргументы сигналов обратной связи ( аргументы обратной связи ).

Логарифмическое уравнение (1.4.28) является внешней функцией по отношению к функциям A и B. В результате эмиссионное уравнение выглядит так:

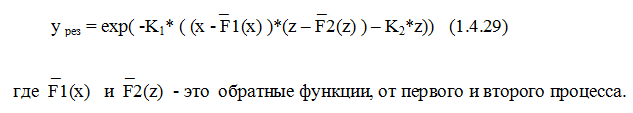
Первый процесс – электрический – это закон «3/2». Он так и представлен в модели, но имеет эмпирический вид:

F1(Ua) = Ia = 9.215e-5 * Ua ^3/2

где:

Ia – ток анода в Амперах,

Ua – напряжение на аноде в Вольтах.

Обратная функция будет иметь вид:

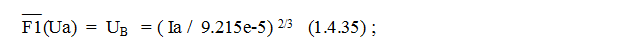
Второй процесс – тепловой - имеет эмпирический вид:

F2(T) = Ia = exp( 1.047e-2 * T - 27.325 )

где:

Ia – ток анода в Амперах,

T - температура катода в Кельвинах.

Обратная функция будет иметь вид:

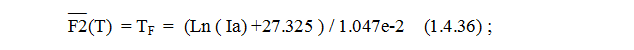
Так как мы моделируем взаимосвязь этих двух процессов, при моделировании ничто не препятствует нам использовать уравнение Ричардсона-Дэшмана, но пока ограничимся эмпирическим вариантом ( очень сложно вычислять обратную функцию от закона Ричардсона-Дэшмана! )

Составим эмиссионное уравнение:

Определим K₁ как К_T, K₂ - как U_D. Далее:

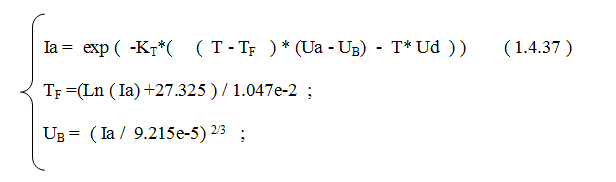
где:

K_T = 0,0956

U_D = 0.01

T > T_F

K_T и U_D - коэффициенты, регулирующие кривизну участка перехода между процессами,

T_F и U_B - обратные функции процессов A и B.

На основе соотношения (1.4.37), применяя подпрограмму Midi, можно построить графики вольт-амперных и кельвин-амперных характеристик. На рис. 1.4.31 представлен график с аргументом Ua:

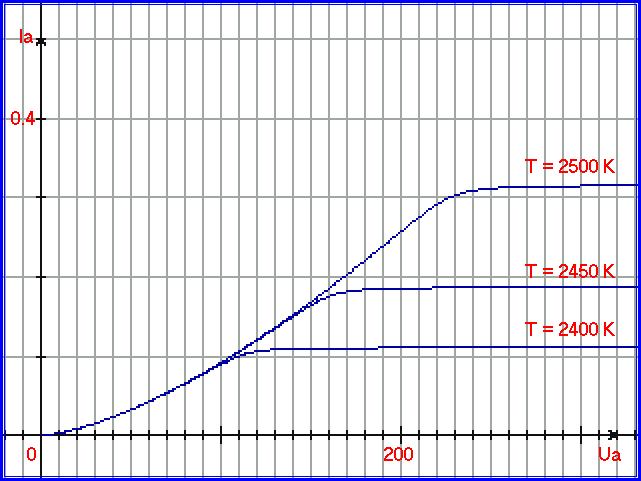
Рис. 1.4.31. График, иллюстрирующий двухмерный процессовый переход для процессов Ia=A = F1(Ua) = 9.215e-5 * Ua (3/2) и Ia = B= F2(T) = exp( 1.047e-2 * T - 27.325 ). Внешняя функция - эмиссионное уравнение. Ось аргумента - в Вольтах, ось функции - в Амперах.

Для построения графика 1.4.31 использовалась подпрограмма Midi2_012, текст подпрограммы приведён ниже:

procedure MidI2_012(x,z:real;var y:real;var c0:integer);var Ymax, Ymin, X0, E: real; Kt,Ub,Ud,Uf,Tf:real; A,B,C,D:real;begin c0:=0; E:=0.000001; Ymax:=exp( (z-0.01)*0.01047-27.325 ); // прямая функция для z Ymin:=0; Kt:=0.0956; Ud:=0.01; repeat begin y:=(Ymax+Ymin)/2; Tf:= (Ln(y)+27.325)/ 0.01047; // обратная функция для z Ub:= power( ( exp( Ln(y)) / 9.216e-5) , (2/3)); // обратная функция для x Uf:=Ub+Ud; if y<=0 then begin c0:=1; // код ошибки break; end; A:=Ln(y); B:=A/(-Kt); C:=B+z*Ud; D:=z-Tf; if D=0 then begin c0:=2; // код ошибки break; end; X0:=(C/D)+Ub; // поэтапное вычисление х ( или Ua ) if X0 > x then Ymax:=y else Ymin:=y; end until (X0+E > x) and (X0-E < x);end;

Та же подпрограмма использовалась при построении семейства кельвин-амперных характеристик с аргументом T (температура катода) на рис. 1.4.32:

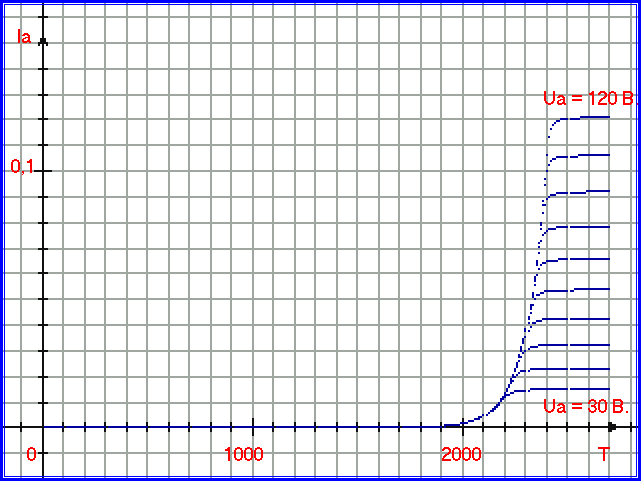
Рис. 1.4.32. График, иллюстрирующий двухмерный процессовый переход для процессов Ia=A = F1(Ua) = 9.215e-5 * Ua (3/2) и Ia = B= F2(T) = exp( 1.047e-2 * T - 27.325 ). Внешняя функция - эмиссионное уравнение. Ось аргумента (температура катода) - в Кельвинах, ось функции - в Амперах.

Заключение.

В данной работе рассмотрены следующие математические разделы:

Теория обратных связей.
Теория перехода процессов.
В главе 1.4.4.2.2 установлена взаимосвязь между функциями с обратными связями и функциями, описывающими переход процессов.
В качестве примеров в главах 1.4.5.2.3 и 1.4.5.2.4 рассмотрены переходы процессов для полупроводникового диода и вакуумного диода, имеющие в качестве внешней функции эмиссионное уравнение.

Данная работа может найти применение для создания физической теории и построения математических моделей ВАХ электронных приборов.

<20 21 222324 25 26 >

Дата добавления: 2021-04-21; просмотров: 245;