Функция, моделирующая результирующее сопротивление в схеме с параллельным соединением резисторов.

В качестве примера рассмотрим сначала схему:

Рис. 1.4.10. Схема двух параллельно соединённых резисторов.

Величина резистора R1 = A, величина резистора R2 = B, где A и B являются некоторыми функциями ( процессами ). Если величины резисторов R1 = A = const и R2 = B = const, то мы моделируем именно 2 резистора, включенные параллельно. Тогда результирующее сопротивление на разъёмах 1 и 2 определяется известной формулой:

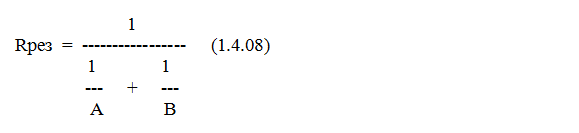
Величины Rрез здесь меньше меньшей величины у резисторов - формула (1.4.08) несёт в себе принцип минимизации результата. По внешнему виду она похожа на рычажные весы, поэтому для краткости будем называть её « формулой весов ». Эта формула действительно «взвешивает» две функции A и B и выдаёт результат, меньший меньшего - происходит переход от процесса к процессу по принципу приближения к минимуму от этих двух процессов.

Если параллельные резисторы R1 и R2 имеют ещё и функциональную зависимость от параметра P, то мы получим следующую схему:

Рис. 1.4.11. Схема двух параллельно соединённых резисторов, функционально зависимых от параметра P (в общем случае A и B - разные функции).

Вариант на рисунке 1.4.11 уже требует дополнительного описания:

величина резистора R1 = A = F1(P),

величина резистора R2 = B = F2(P).

Результирующее значение находим по формуле:

Поскольку функциональные зависимости A и B здесь зависят только от одной переменной P, то такой процессовый переход мы назовём «одномерным».