Зависимости ВАХ полупроводникового диода от температуры согласно уравнению Шокли. Несостоятельность уравнения Шокли.
Посмотрим, как должны вести себя ВАХ при изменении температуры Т согласно уравнению Шокли. Для прямого тока PN-перехода уравнение Шокли имеет вид:
Iа = Is * exp( (β*e*Uа)/(k*T) )
Можно преобразовать это выражение к виду:
Iа = exp ( K*Uа + B ),
где K = (β *e)/(k*T) = β*39.57065 при T = 293 Кельвин,
B = Ln ( Is ).
Для диода КД213А мы установили ( при T= 293 Кельвин ) , что
β = 0,753
K =29,8
B = - 18,7
Параметр B не должен влиять на наклон прямой, однако в современных моделях этот параметр вдруг становиться температурно-зависимым, что неверно. Температура в уравнении Шокли определена только в знаменателе выражения (β *e)/(k*T). Построим графики при температурах 10, 20 и 30 градусов Цельсия для диода КД213А по уравнению Шокли, считая параметр В на данном участке температур неизменным и равным -18,7. Как мы уже определили, параметр B не должен влиять на наклон прямой, иначе В становиться зависимым и от Uа. На рис. 1.4.4 построены графики при температурах 10, 20 и 30 градусов Цельсия для диода КД213А по уравнению Шокли (график для температуры 10 градусов Цельсия построен красными точками, 20 градусов – зелёными, 30 градусов – сиреневыми). Графики построены поверх ВАХ экспериментальных данных для диода КД213А при температуре 20 градусов Цельсия (синие точки):
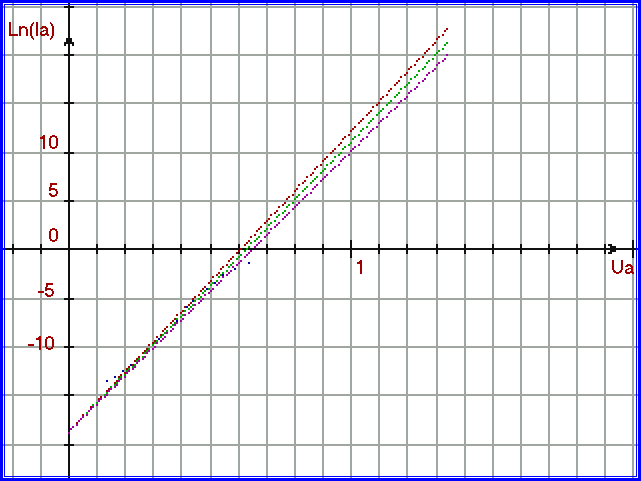
Рис. 1.4.4. Зависимость ВАХ от температуры согласно уравнению Шокли (графики построены поверх экспериментальных данных в полулогарифмическом масштабе, на оси Ua одно деление равно 100 мВ).
Наблюдения, которые можно сделать из рис. 1.4.4:
1. Графики уравнения Шокли имеют вид расширяющегося пучка прямых от точки, расположенной на оси ординат.
2. Более низкие температуры соответствуют более высокому току при одном и том же Ua.
Проведённые эксперименты с температурами показывают, что данные свойства уравнения Шокли не соответствуют свойствам ВАХ реальных полупроводниковых диодов. График 2 демонстрирует серьёзную ошибку уравнения Шокли, выражающейся в противоположном направлении монотонности функции тока в зависимости от температуры.
Проведённый эксперимент и обнаруженная ошибка в уравнении Шокли заставили меня задуматься об истинной природе наблюдаемого явления. Построенные мной в дальнейшем математические модели позволили мне обнаружить в свойстве односторонней проводимости ( ОП ) полупроводникового диода два физических процесса – тепловой и электрический. Это явление родственно эффекту Пельтье. Полупроводниковые элементы Пельтье, как известно, обладают PN-переходами с более «узкой запрещённой зоной», что позволяет существовать обратному току. Термодинамика полупроводниковых элементов Пельтье используется при конструировании холодильников и электро-термогенераторов. Термодинамика же полупроводникового диода до сих пор не изучена. Попытку её изучить и была мной предпринята. В процессе моделирования было получено уравнение, также являющиеся «эмиссионным», но обладающая некоторыми отличительными чертами:
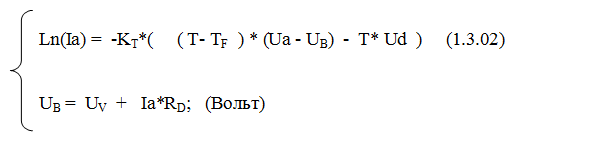
Здесь:
KT = 0,0956 (Кельвин -1*Вольт -1 ),
TF =605,2 (Kельвин),
UD = 0,276 (Вольт),
UV = 0,885 (Вольт),
RD = 0,25 (Ом),
Т – температура окружающей среды (Кельвин),
T < TF,
UF = UB + UD (Вольт),
T – температура окружающей среды ( или температура PN - перехода ),
Ua – напряжение, приложенное к PN-переходу,
Ia – ток анода.
Сразу возникают вопросы:
- Что такое «эмиссионное» уравнение?
- С чем связана такая форма математической модели?
- Возможны ли другие варианты моделирования?
В своей работе я попытался ответить на эти вопросы. Так возникла математическая теория процессового перехода как системы с отрицательной обратной связью (ООС).
Решение эмиссионного уравнения обеспечивается алгоритмами программирования. Программирование осуществлялось в системе Delphi на языке Pascal.
Обратные связи. Свойства экспоненциальной функции в двухполюснике, состоящего из идеального диода и резистора (резистор по своей величине соответствует коэффициенту отрицательной обратной связи).
Дата добавления: 2021-04-21; просмотров: 576;











