ФИЗИКО-ХИМИЧЕСКИЕ СВОЙСТВА УГЛЕВОДОРОДНЫХ ГАЗОВ

Нефтяной газ при нормальных условиях содержит неполярные углеводороды - смесь углеводородовв от С₁ до С₄: метан, этан, пропан, изо-бутан и н-бутан. С точки зрения физики к ним можно применять законы для идеальных систем. С точки зрения математики – это аддитивная система. Следовательно, для оценки свойств нефтяного газа (при нормальных или стандартых условиях) применимы аддитивные методы расчётов физико-химических и технологических параметров (П_смеси):

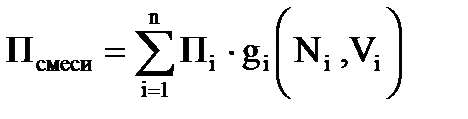, (2.3)

где g_i – весовая доля;

N_i – мольная доля;

V_i – объёмная доля;

П_i – параметр i-го углеводорода или неуглеводородного компонента.

Например, плотностьсмеси газов рассчитывается следующим образом:

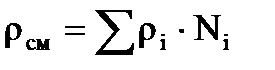. (2.4)

Плотность газа можно расчитать через отношение молекулярной массы газа (M_i) к мольному объему (V_м). Например, для нормальных условиях (н.у.):

r_г = M_i / 22,414. (2.5)

Нефтяной газ представлен в виде смеси углеводородов, поэтому для оценки его физико-химических свойств по формуле (2.3) необходимо знать, как выражается состав смеси.

Массовая доля (g_i) – отношение массы i-го компонента (m_i), содержащегося в системе к общей массе системы:

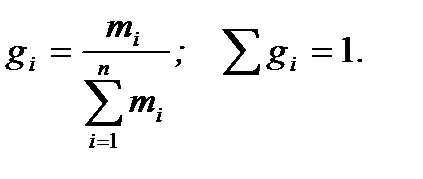(2.6)

Молярная (мольная) доля (N_i) – отношение числа молей i-го компонента (т_ш) к общему числу молей в системе:

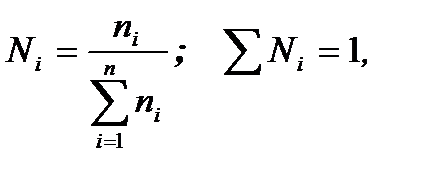
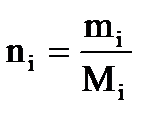, (2.7)

где m_i – масса i-го компонента;

М_i – молекулярный вес i-го компонента.

Из соотношений (2.6 – 2.7) легко найти выражения для пересчетов массового и мольного составов:

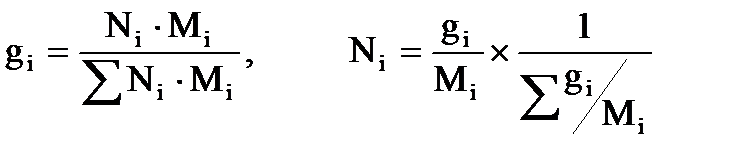(2.8)

Объёмная доля – это доля (V_i), которую занимает компонент в объёме системы и с учетом выражений (2.5 – 2.8) можно найти взаимосвязь ее с массовым и мольным составами:

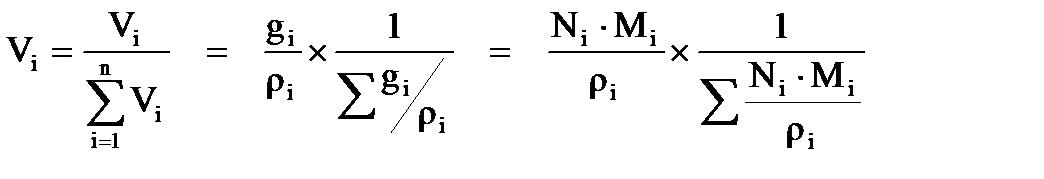(2.9)

Для идеального газа соблюдается соотношение: объемная доля компонента (V_i ) равна мольной доли компонента (N_i), V_i = N_i , как следствие закона Авогадро. Для идеальной системы, как нефтяной газ, состав его можно рачитать на основе любых данных: масс компонентов, объемов, плотностей, парциальных давлений и др., см. раздел "Практикум для самостоятельной работы".

Молекулярная масса смеси рассчитывается по принципу аддитивности для смесей, состав которых выражен в мольных или объемных долях (2.10, левое выражение). Для смесей, состав которых выражен в ммассовых процентах по формуле 2.10, правое выражение:

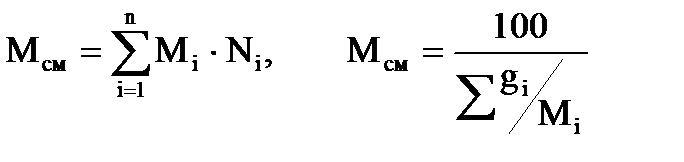(2.10)

Относительная плотность газа расчитывается по отношению к плотности воздуха:

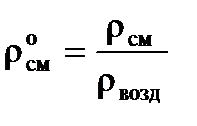. (2.11)

Для нормальных условий (н.у.) ρ_возд » 1,293; для стандартных условий (с.у.) ρ_возд » 1,205.

Если плотность газа (ρ_о) задана при атмосферном давлении = 0,1013 МПа, то пересчёт её на другое давление (Р) при той же температуре для идеального газа производится по формуле:

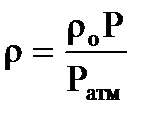. (2.12)

Смеси идеальных газов характеризуются аддитивностью парциальных давлений и парциальных объёмов.

Для идеальных газов давление смеси равно сумме парциальных давлений компонентов (закон Дальтона):

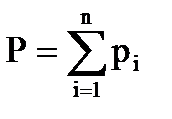, (2.13)

где Р – давление смеси газов;

р_i – парциальное давление i-го компонента в смеси,

или

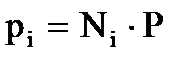. (2.14)

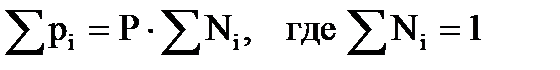. (2.15)

Т. е. парциальное давление газа в смеси равно произведению его молярной доли в смеси на общее давление смеси газов (2.14).

Аддитивность парциальных объёмов компонентов газовой смеси выражается законом Амага:

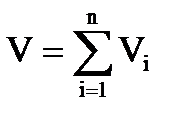, (2.16)

где V – объём смеси газов;

V_i – объём i-го компонента в смеси.

или анологично уравнениям (2.14 – 2.15) выражением 2.17:

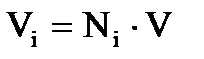. (2.17)

Для определения многих физических свойств природных газов используется уравнение состояния.

Уравнением состояния называется аналитическая зависимость между параметрами, описывающими изменение состояние вещества. В качестве таких параметров используется давление, температура, объём.

Состояние газа при нормальных и стандартных условиях характеризуется уравнением состояния Менделеева-Клайперона:

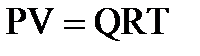, (2.18)

где Р – абсолютное давление, Па;

V – объём, м³;

Q – количество вещества, кмоль;

Т – абсолютная температура, К;

R – универсальная газовая постоянная, Па×м³/(кмоль×град).

На основе уравнения состояния газа можно рассчитать много параметров для системы нефтяного газа: плотность, мольный объем, количество молекул, число молекул, парциальные давления и др., если рассматривать уравнение состояния газа для 1 моля, т.е., Q = ∑N_i и PV = ∑N_iRT, см. раздел "Практикум для самостоятельной работы".

У этого уравнения есть свои граничные условия. Оно справедливо для идеальных газов при нормальном, атмосферном давлении (1 атм) и близких к нормальному давлениях (10-12 атм).

При повышенном давлении газ сжимается. За счёт направленности связи С-Н происходит перераспределение электронной плотности, и молекулы газов начинают притягиваться друг к другу (физическое взаимодействие).

Для учёта этого взаимодействия в уравнение (2.18) вводится коэффициент сверхсжимаемости z, предложенный голландским физиком Ван-дер-Ваальсом, учитывающий отклонения поведения реального газа от идеального состояния:

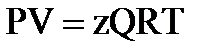, (2.19)

где Q – количество вещества, моль;

z – коэффициент сверхсжимаемости.

Физический смысл коэффициента сверхсжимаемости заключается в расширении граничных условий уравнения Менделеева - Клайперона для высоких давлений.

Коэффициент z зависит от давления и температуры (приведенных, критических давлений и температуры), природы газа.

Критическое давление – давление, при котором газообразный углеводород переходит в жидкое состояние.