Астатизм дискретных систем

Свойство астатизма дискретных систем, как отмечалось выше, аналогично свойству астатизма непрерывных систем. Однако имеется ряд особенностей, обусловленных квантованием переменных по времени.

Определение. Астатической называют дискретную систему, статическая ошибка которой равна нулю. В противном случае систему называют статической. ■

Приведенному определению удовлетворяют два типа дискретных систем. У систем первого типа ошибка при постоянном входном воздействии равна нулю как в моменты времени, кратные периоду квантования T, так и во все остальные. В то же время у астатических систем второго типа ошибка при постоянном входном воздействии равна нулю только в моменты времени, кратные периоду квантования T, а во все остальные моменты ошибка не является нулевой. Эти свойства дискретных систем связаны с различными способами обеспечения математических условий астатизма, которые присущи дискретным системам.

Астатические дискретные, как и непрерывные, системы могут иметь астатизм различных порядков. Порядок астатизма в случае дискретных систем, также как и в непрерывном случае, можно оценивать либо по заданной структурной схеме, либо по передаточной функции по ошибке, либо по передаточной функции системы в разомкнутом состоянии (при главной единичной обратной связи), либо по передаточной функции системы в замкнутом состоянии.

Признак астатизма дискретных систем по 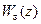.Изображение сигнала ошибки, вызванной, например, воздействием g_k, можно записать при нулевых начальных условиях

следующим образом:

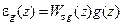, (15.55)

где 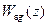– передаточная функция системы по ошибке, вызванной воздействием g_k.

Подчеркнем, что ошибки по тому или иному воздействию определяются лишь для устойчивых систем управления, поэтому знаменатель передаточной функции 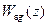всегда имеет корни по модулю меньше единицы. Так как свойство астатизма определяется величиной статической ошибки, т.е. при постоянном воздействии, то можно полагать, что

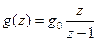. (15.56)

Поэтому из (15.55) и (15.56) выводим

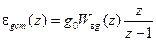. (15.57)

Из этого равенства и свойств Z-преобразования следует вывод: для того, чтобы статическая ошибка дискретной системы равнялась нулю, необходимо и достаточно, чтобы соответствующая передаточная функция по ошибке 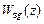содержала в качестве множителя двучлен (z – 1), т.е.

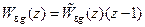, (15.58)

где 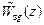– некоторая дробь, все полюсы которой по модулю меньше единицы.

При выполнении условия (15.58) из (15.57) выводим

.

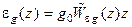Применяя к этому выражению теорему о предельном значении (см. стр. 354), получим с учетом указанного выше свойства полюсов :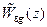

.

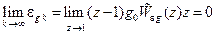Итак, если условие (15.58) выполнено, то дискретная система является астатической по задающему воздействию g_k. Поэтому равенство (15.58) является выраженным через передаточную функцию по ошибке признаком астатизма дискретных систем по задающему воздействию.

Аналогичный вид 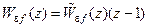имеет и условие астатизма дискретных систем управления к дискретному возмущению .

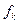Признаки астатизма дискретных систем по 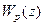. Вид этих признаков зависит от типа системы, от вида обратной связи, и от того является ли рассматриваемое воздействие задающим или возмущающим. Рассмотрим здесь случай, когда система является системой стабилизации, программного управления или следящей, а обратная связь является единичной и отрицательной, т.е. тот случай, когда передаточная функция по ошибке, обусловленной задающим воздействием g_k, определяется выражением

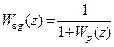. (15.59)

Нетрудно видеть, что в этом случае по отношению к задающему воздействию g_k условие (15.58) выполняется, если

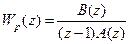, (15.60)

где 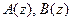– некоторые полиномы, причем .

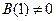Основной особенностью выражения (15.60) является наличие множителя (z – 1) в знаменателе W_p(z). Поэтому выражение (15.60) является выраженным через передаточную функцию W_p(z)признаком астатизма дискретных систем по задающему воздействию.

Передаточная функция W_p(z), в частности, будет иметь вид (15.60), если приведённая непрерывная часть дискретной системы содержит хотя бы один чистый интегратор. При этом структурную схему такой системы можно представить так, как показано на рис. 15.16. В установившемся режиме рассогласование системы с W_p(z) (15.60), вызванное постоянным задающим воздействием, а также вынужденная составляющая отклонения 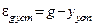, будут равны нулю во все моменты времени как кратные периоду квантования T , так и в остальные моменты времени (рис. 15.17).

Пример 15.17. Оценить свойство астатизма систем, рассмотренных в примерах 15.2 и 15.15, по отношению к задающему воздействию. При этом считать, что обратная связь системы, рассмотренной в примере 15.15, единичная и отрицательная.

Решение. В системе, рассмотренной в примере 15.2, обратная связь единичная, а непрерывная часть системы не содержит интеграторов, поэтому данная система является статической по отношению к задающему воздействию. При указанном в задании условии, передаточная функция системы, рассмотренной в примере 15.15, в разомкнутом состоянии имеет вид

.

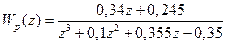С помощью MATLAB легко найти, что корни знаменателя этой функции равны: 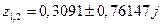; 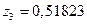. Следовательно, эта функция не удовлетворяет условию (15.60). Поэтому система, рассмотренная в примере 15.15, также является статической. Этот вывод подтверждается и графиком переходной функции данной системы, который приведен на рис 15.15. ■

Множитель (z – 1) в знаменателе W_p(z) (15.60) можно получить и при отсутствии интегратора в непрерывной части дискретной системы. Для этого достаточно включить сумматор в алгоритм работы ЦВМ, вычисляющей по отклонению 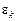значения управляющего воздействия (управления) в каждом периоде квантования. Однако в этом случае отклонение в установившемся режиме (при 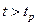) будет равно нулю, т.е. 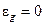, только при 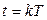, а при 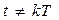отклонение системы 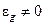. При использовании сумматора с целью обеспечения астатизма оценку реальной ошибки системы управления непрерывным объектом необходимо в обязательном порядке проводить путём моделирования системы. При этом непрерывная часть может моделироваться либо непрерывными моделирующими установками, либо с помощью ЦВМ, но путем интегрирования непрерывных дифференциальных уравнений объекта. Дискретная часть системы может моделироваться по разностным уравнениям.

По отношению к возмущению f(t), приложенному к прямой связи дискретной системы, условия астатизма имеют вид, аналогичный непрерывному случаю: или дискретная часть содержит сумматор или непрерывная часть содержит интегратор между точкой измерения отклонения и точкой приложения возмущения f(t).

Признак астатизма дискретных систем поW_yg(z).Ограничимся здесь случаем задающего воздействия и предположим, что передаточная функция некоторой устойчивой дискретной системы по этому воздействию представлена в виде

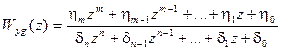. (15.61)

Признак астатизма рассматриваемой системы по задающему воздействию 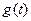при известной W_yg(z) (15.61) имеет вид

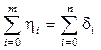. (15.62)

Данное условие автоматически выполняется, в частности, при наличии интегратора в непрерывной части системы или сумматора в дискретной части системы и отрицательной единичной обратной связи, как показано на рис. 15.16.

Пример 15.18. Оценить свойство астатизма системы, рассмотренной в примере 15.15, по её передаточной функции W_yg(z).

Решение. Сумма коэффициентов числителя передаточной функции заданной системы равна 0,585, а сумма коэффициентов знаменателя – 1,69. Следовательно, и в соответствии с критерием (15.62), рассматриваемая система является статической.

Условие астатизма ν-го порядка.Система обладает астатизмомν-го порядка по отношению к некоторому воздействию, если её ошибка, вызванная полиномиальным воздействием степени ν – 1, равна нулю, а ошибка, вызванная полиномиальным воздействием степени ν, не равна нулю, но постоянна по величине. Приведённое выше определение астатической системы, очевидно, соответствует случаю астатизма первого порядка, а определение статической системы – случаю астатизма нулевого порядка.

Полностью повторяя рассуждения и выкладки, проведенные при выводе условия (15.58), можно установить, что признак астатизма ν-го порядка к задающему воздействию в случае дискретных систем управления имеет вид

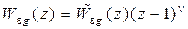, (15.63)

где 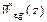– также некоторая рациональная дробь, все нули знаменателя которой по модулю строго меньше единицы.

Условие (15.63) также будет обеспечено при наличии либо ν чистых интеграторов в непрерывной части, либо ν сумматоров в дискретной части системы, либо различной комбинацией тех и других элементов. При этом ошибка системы, вызванная полиномиальным воздействием ν-ой степени, будет постоянной, а воздействием (ν – 1)-й степени и ниже – нулевой. В зависимости от способа реализации условия (15.63) ошибка системы будет нулевой или постоянной либо во все моменты времени (если в системе имеется ν чистых интеграторов), либо только в дискретные моменты времени в противном случае.