Устойчивость дискретных систем
Необходимые и достаточные условия.Как и в непрерывном случае, устойчивость является важнейшим свойством дискретных систем. В линейном случае исследование их устойчивости также осуществляется на основе характеристического уравнения. В связи с этим заметим, что если непрерывная часть дискретной системы полная, то степень знаменателя передаточной функции 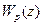 (15.23) должна быть равна степени знаменателя
(15.23) должна быть равна степени знаменателя  или размеру матрицы
или размеру матрицы 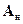 уравнений в переменных состояния (15.4) непрерывной части (т.е. без учета импульсного элемента). В этом случае характеристический полином замкнутой системы определяется выражением
уравнений в переменных состояния (15.4) непрерывной части (т.е. без учета импульсного элемента). В этом случае характеристический полином замкнутой системы определяется выражением
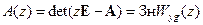 , (15.46)
, (15.46)
где матрица А определяется равенствами (15.14), (15.28) или (15.30), а передаточная функция Wyg(p) – вторым выражением (15.18) или другим, эквивалентным ему. ■
Другими словами, если непрерывная часть системы полная, то характеристический полином замкнутой системы может быть найден как знаменатель любой передаточной функции исследуемой дискретной системы в замкнутом состоянии. Если же непрерывная часть импульсной системы неполная, то характеристический полином соответствующей дискретной системы может быть найден только по уравнениям в переменных состояния (15.14), как det(zE – A), где А – системная матрица.
В общем случае характеристическое уравнение дискретных систем имеет вид
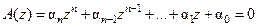 , (15.47)
, (15.47)
где  – порядок системы,
– порядок системы, 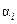 – коэффициенты (обычно постоянные числа),
– коэффициенты (обычно постоянные числа), 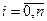 . В соответствии с определением Z-преобразования переменная
. В соответствии с определением Z-преобразования переменная 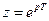 , поэтому корни
, поэтому корни 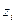 уравнения (15.47) можно всегда представить в виде
уравнения (15.47) можно всегда представить в виде  . Здесь
. Здесь 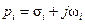 – корни характеристического уравнения некоторой непрерывной системы. С учётом этого равенства имеем
– корни характеристического уравнения некоторой непрерывной системы. С учётом этого равенства имеем 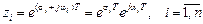 , т.е. реальная часть корней
, т.е. реальная часть корней 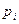 влияет лишь на модуль корней на плоскости
влияет лишь на модуль корней на плоскости 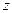 , так как
, так как 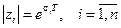 .
.
С другой стороны, условие устойчивости на плоскости комплексного переменного p, как известно, имеет вид 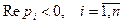 . Отсюда следует, что условие устойчивости линейных дискретных систем на плоскости z имеет вид
. Отсюда следует, что условие устойчивости линейных дискретных систем на плоскости z имеет вид
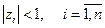 . (15.48)
. (15.48)
Геометрически это условие означает, что на комплексной плоскости z все корни характеристического уравнения (15.47) устойчивой линейной дискретной системы располагаются в круге единичного радиуса (на рис. 15.13 этот круг заштрихован).
Пример 15.8.Исследовать устойчивость системы с характеристическим полиномом 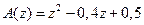 .
.
Решение. Корни заданного полинома, очевидно, равны 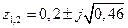 . Их модули
. Их модули  . Следовательно, заданная дискретная система является устойчивой. ■
. Следовательно, заданная дискретная система является устойчивой. ■
Критерий Шура-Кона. Для исследования устойчивости дискретных систем по коэффициентам характеристического уравнения (15.47) применяется специальный критерий, с помощью которого проверяется выполнимость условия (15.48). Этот критерий называется критерием Шура-Кона. Если некоторый полином (15.47) удовлетворяет этому критерию, то все его корни по модулю меньше единицы.
Для применения критерия Шура-Кона сначала необходимо из коэффициентов характеристического полинома (15.47) исследуемой системы составить таблицу Шура-Кона.
Таблица 15.2

| 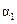
| 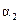
| 
| 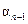
| 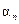
| |
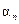
| 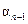
| 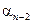
| 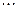
| 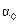
| ||
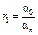
| 
| 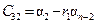
| 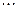
| 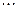
| 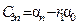
| |
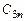
| 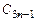
| 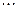
| 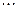
| 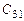
| ||

| 
| 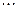
| 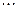
| |||
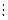
| 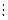
| 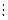
| 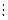
|
Составляется таблица Шура-Кона следующим образом. В первую строку вписываются подряд коэффициенты заданного полинома (15.47), начиная с младшего 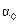 . Во вторую строку вписываются те же коэффициенты, но в обратном порядке. Следующая строка вычисляется в соответствии с правилом заполнения третьей и последующих строк таблицы Рауса (см. § 4.3). Затем полученные коэффициенты вписываются в следующую строку, но в обратном порядке. Далее описанный процесс повторяется до получения коэффициента rn.
. Во вторую строку вписываются те же коэффициенты, но в обратном порядке. Следующая строка вычисляется в соответствии с правилом заполнения третьей и последующих строк таблицы Рауса (см. § 4.3). Затем полученные коэффициенты вписываются в следующую строку, но в обратном порядке. Далее описанный процесс повторяется до получения коэффициента rn.
После заполнения таблицы Шура-Кона применяется собственно критерий Шура-Кона, который формулируется следующим образом.
Критерий Шура-Кона.Если в таблице Шура-Кона все коэффициенты  ,
,  , то дискретная система с заданным характеристическим уравнением (15.47) асимптотически устойчива. ■
, то дискретная система с заданным характеристическим уравнением (15.47) асимптотически устойчива. ■
Пример 15.9. Исследовать с помощью критерия Шура-Кона устойчивость дискретной системы с характеристическим полиномом 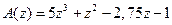 .
.
Решение. Составим сначала таблицу Шура-Кона в соответствии с описанными выше правилами:
Таблица 15.3
| –1 | –2,75 | |||
| –2,75 | –1 | |||
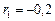
| 
| 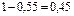
| 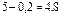
| |
| 4,8 | 0,45 | –2,55 | ||
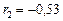
| 0,69 | 3,45 | ||
| 3,45 | 0,69 | |||
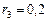
|
Так как в табл. 15.3 все  , то в соответствии с критерием Щура-Кона рассматриваемая система асимптотически устойчива. ■
, то в соответствии с критерием Щура-Кона рассматриваемая система асимптотически устойчива. ■
Применение критерия Гурвица. Критерий Шура-Кона является численным критерием. Для решения же задач синтеза систем или для исследования влияния параметров на свойства систем целесообразно применять аналитические критерии. К таким критериям относится, например, рассмотренный выше критерий Гурвица. Однако для того, чтобы иметь возможность применить его к исследованию дискретных систем, необходимо сначала провести замену переменной в уравнении (15.47) по формуле
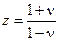 , (15.49)
, (15.49)
где ν – новая комплексная переменная. Данная замена преобразовывает круг на плоскости z в левую полуплоскость плоскости ν, поэтому условие устойчивости на плоскости ν имеет вид Re ν < 0, что и позволяет применить к полиному относительно переменной 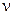 критерий Гурвица (см. § 4.3).
критерий Гурвица (см. § 4.3).
Критерий Гурвица. Если характеристический полином 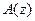 преобразован к
преобразован к 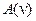 , и последний удовлетворяет критерию Гурвица (§ 4.3), то дискретная система с данным полиномом
, и последний удовлетворяет критерию Гурвица (§ 4.3), то дискретная система с данным полиномом 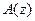 асимптотически устойчива. В противном случае она является неустойчивой. ■
асимптотически устойчива. В противном случае она является неустойчивой. ■
Пример 15.10. Исследовать устойчивость дискретной системы с характеристическим полиномом 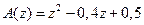 .
.
Решение. Выполняя замену согласно (15.49), получим
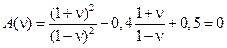 .
.
Отсюда
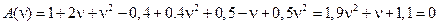 .
.
Так как все коэффициенты полученного полинома положительные, а его степень равна двум, то он удовлетворяет критерию Гурвица (см. § 4.3), следовательно, рассматриваемая дискретная система устойчива, т.е. корни её характеристического уравнения удовлетворяют условию (15.48). ■
В частности, критерий Гурвица позволяет найти критические по устойчивости значения параметров дискретных систем.
Применение критерия Михайлова. Для оценки устойчивости дискретных систем с помощью критерия Михайлова необходимо построить годограф Михайлова
 ,
, 
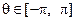 , (15.50)
, (15.50)
где 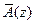 – нормированный по старшей степени
– нормированный по старшей степени  характеристический полином (15.47) исследуемой системы.
характеристический полином (15.47) исследуемой системы.
Критерий Михайлова. Дискретная система с характеристическим полиномом (15.47) является устойчивой, если годограф Михайлова (15.50) при изменении  от
от 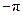 до
до 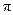 , начинаясь на вещественной оси, обходит последовательно вокруг точки
, начинаясь на вещественной оси, обходит последовательно вокруг точки 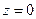 в положительном направлении (против часовой стрелки)
в положительном направлении (против часовой стрелки)  квадрантов. В противном случае, система является неустойчивой. ■
квадрантов. В противном случае, система является неустойчивой. ■
Отметим, что если годограф Михайлова обходит все квадранты последовательно, т.е. порядок обхода не нарушается, то достаточно длинный отрезок прямой, проведенный из точки 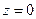 под любым углом, пересекает годограф в n точках. В противном случае критерий Михайлова не выполняется.
под любым углом, пересекает годограф в n точках. В противном случае критерий Михайлова не выполняется.
Пример 15.11. Оценить устойчивостьдискретной системы с характеристическим полиномом 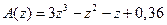 с помощью критерия Михайлова.
с помощью критерия Михайлова.
Решение.В данном случае полином 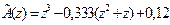 . Полагая
. Полагая 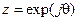 , получим
, получим 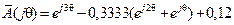 . Заменяя в выражении для
. Заменяя в выражении для 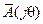 функцию
функцию 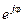 по формуле Эйлера
по формуле Эйлера 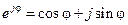 и изменяя
и изменяя  от
от 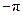 до
до 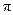 , построим график, приведённый на рис. 15.14.
, построим график, приведённый на рис. 15.14.
Как видно, рассматриваемая система является устойчивой, так как годограф Михайлова обходит последовательно вокруг точки 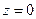 против часовой стрелки 12 квадрантов (т.е. отрезок прямой, проведенный из точки
против часовой стрелки 12 квадрантов (т.е. отрезок прямой, проведенный из точки 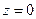 под любым углом, пересекает годограф в 3 точках). ■
под любым углом, пересекает годограф в 3 точках). ■
Запасы устойчивости дискретных систем.Для оценки запасов устойчивости дискретных систем, как и непрерывных, применяются различные оценки.
Определение. Степень устойчивости дискретных систем на плоскости z равна разности
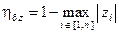 , (15.51)
, (15.51)
где  – корни характеристического уравнения A(z) (15.47) замкнутой дискретной системы.
– корни характеристического уравнения A(z) (15.47) замкнутой дискретной системы.
На комплексной плоскости р соответствующая степень устойчивости дискретной системы определяется по формуле
 . (15.52)
. (15.52)
Здесь T – период квантования по времени в исследуемой системе.
Если система является неустойчивой, то запасы устойчивости не определяются.
Пример 15.12. Найти степени устойчивости системы, которая описывается уравнением
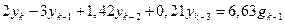 , (15.53)
, (15.53)
а период квантования T = 0,1с.
Решение. Корни характеристического уравнения системы (15.53) (найдены с помощью функции roots из пакета MATLAB) равны 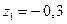 ;
; 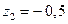 ;
;  . Следовательно, в соответствии с выражениями (15.51) и (15.52), степень устойчивости на плоскости z данной системы
. Следовательно, в соответствии с выражениями (15.51) и (15.52), степень устойчивости на плоскости z данной системы 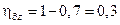 , а на плоскости p –
, а на плоскости p – 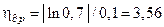 . ■
. ■
Запасы устойчивости дискретных систем можно оценить и с помощью критерия устойчивости Михайлова.
Определение. Запас устойчивости дискретных систем по критерию Михайлова 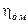 – это радиус окружности с центром в точке
– это радиус окружности с центром в точке 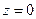 , которую можно вписать внутрь годографа Михайлова. Если критерий Михайлова не выполняется, то запас устойчивости
, которую можно вписать внутрь годографа Михайлова. Если критерий Михайлова не выполняется, то запас устойчивости 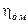 не определяется.
не определяется.
Например, дискретная система, годограф Михайлова которой приведён на рис. 15.14, имеет запас устойчивости 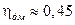 .
.
Дата добавления: 2022-05-27; просмотров: 337;










