Зеркальные отклоняющие системы

Существует большое количество конструкций ОС. Перемещения лазерного луча (или его проецирование) может быть реализовано с помощью различных оптических элементов: линз, зеркал, призм, элементов нелинейной оптики и других. Зеркальные ОС получили наибольшее распространение. В таких системах перемещение луча по изделию осуществляется одним или несколькими плоскими зеркалами. Плоское зеркало является простейшей оптической системой, которое обеспечивает получение идеального изображения:

- отсутствует сферическая аберрация;

- размеры изображения равны размерам предмета;

- сохраняется гомоцентричность после очередного отражения.

Всем другим системам, кроме вышеперечисленных, присущ еще один серьезный недостаток – размытие изображения, уменьшение концентрации и, как следствие, снижение эффективности использования лазерного излучения. Для отклонения луча плоское зеркало поворачивают или смещают вдоль оптической оси. При повороте плоского зеркала отраженный луч поворачивает на удвоенный угол .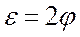

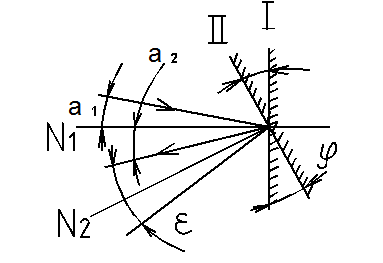
Рисунок 4.36 – Схема поворота плоского зеркала. 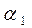- угол падения луча на зеркало, 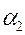- угол поворота нормали зеркала.

Смещение плоского зеркала по нормам вызывает смещение изображения на величину

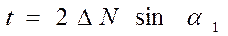. (4.70)

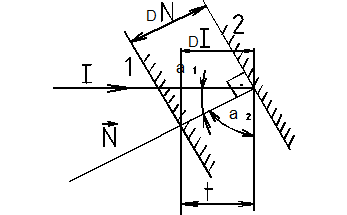
Рисунок 4.37 – Схема смещения плоского зеркала.

ри смещении плоского зеркала по оси падающего луча на 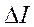изображение смещается на величину

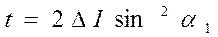, (4.71)

при , ,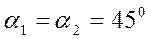

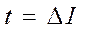где 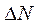- смещение зеркала вдоль нормали;

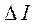- смещение плоского зеркала вдоль оптической оси.

Если сходящийся луч после k отражений выходит из системы плоских зеркал, то для радиус – вектора 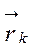текущей точки отраженного луча справедливо выражение:

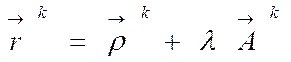, (4.72)

где 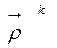- радиус-вектор изображения точки Т^К, предмета Т, отраженной k раз в системе плоских зеркал, относительно полюса О. Последний совпадает с точкой предмета Т;

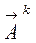- орт выходящего луча после отражения k раз в системе плоских зеркал.

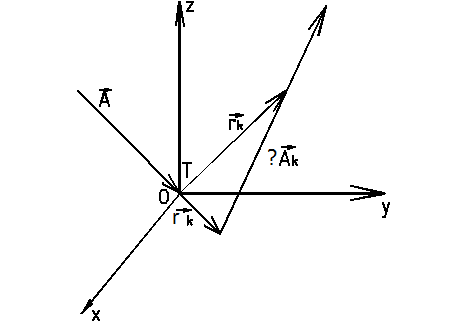
Рисунок 4.38 - Отражение точки и луча от системы плоских зеркал.

Выражение для радиус-вектора изображения точки в системе координат (х₁y₁z₁) для плоского зеркала имеет вид:

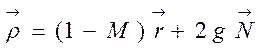, (4.73)

где 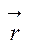- радиус-вектор точки с, вокруг которой вращается каждая из зеркальных систем, относительно точки предмета м;

q – расстояние от точки с до отражающей плоскости зеркала;

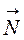- орт направления нормали плоского зеркала;

М – матрица действия плоского зеркала.

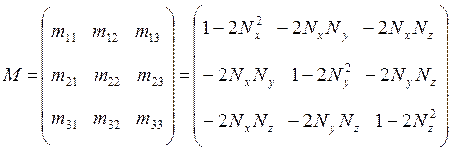(4.74)

где N_x, N_y, N_z – проекции орта 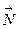на координатные оси.

Матрицу действия плоского зеркала можно найти из формулы:

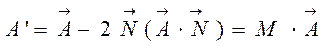. (4.75)