Узел юстировки со сферическим подшипником

Узел юстировки со сферическим подшипником (Рис.4.33) позволяет при той же компактности и сравнительно низкой стоимости, что и узел юстировки с крепежными винтами, значительно повысить точность и увеличить диапазон углов поворота. Юстировка по-прежнему выполняется в 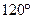координатах.

В такой конструкции зеркало 2 закрепляется во внутреннем кольце 1 сферического подшипника. Внешнее кольцо (6), которое является корпусом юстировочного узла. От осевого смещения внутреннее кольцо подшипника удерживается тремя плоскими пружинами (3). Правые концы, на которых с помощью трех эксцентриковых осей (5) грубой юстировки могут перемещаться вдоль оптической оси. Для точной юстировки используются три винта (4), которые своими концами упираются в среднюю часть плоских пружин (3) и прогибают их с шагом 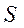. Прогнутая плоская пружина выполняет роль рычага с переменным (в зависимости от величины прогиба) соотношением плеч.

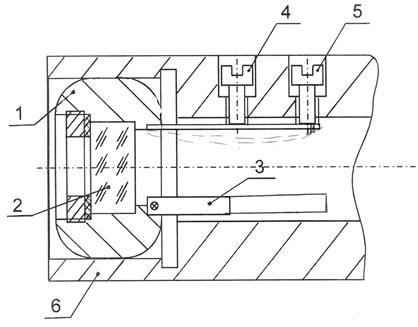
Рис.4.33. Узел юстировки сферическим подшипником.

Чувствительность данного механизма максимальна при малом прогибе пружины и постепенно уменьшается по мере ввертывания винтов (4). Оба юстировочных механизма после заводской выверки пломбируются. Как правило, головки винтов заливают красной эмалью.

4.13 Фокусировка лазерного излучения

Общие положения расчета параметров фокусирующих систем

Лазерное излучение, которое получается на выходе из резонатора, как правило, нельзя использовать для технологических целей. Такое излучение не обеспечивает концентрации энергии, достаточной для фазовых превращений в обрабатываемом материале. Для реализации большинства технологических процессов необходима дополнительная фокусировка лазерного излучения вне лазера. Расчет параметров фокусирующих систем осуществляется на основе положений геометрической оптики. Вспомним основные понятия геометрической оптики, которые необходимы для расчетов оптических систем.

Под световым лучом понимают ось световой трубки, т.е. прямую или ломаную линию.

Пучок лучей, выходящий из одной точки или приходящий в одну точку, называетсягомоцентрическим.

Основные представления геометрической оптики наглядно демонстрируются при прохождении луча через линзу.

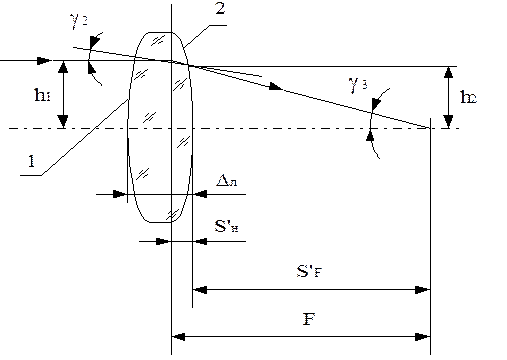
Рисунок 4.34 - Схема прохождения луча через линзу (Н-Н — главная плоскость линзы).

Входной луч проходит на высоте 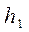параллельно оси линзы ( ). Линза изготовлена из материала с коэффициентом преломления . Радиусы кривизны поверхностей и 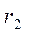системы находятся в воздухе.

После преломления на поверхности 1 угол наклона луча 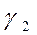к оси линзы

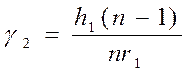. (4.48)

Высота преломления с поверхностью 2

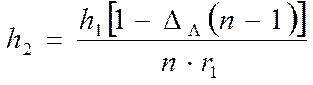. (4.49)

Угол наклона луча, вышедшего из линзы,

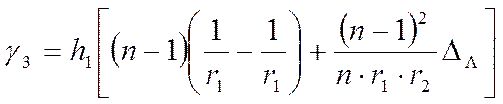. (4.50)

Фокусное расстояние линзы

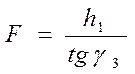. (4.51)

Считая, что лучи параксиальные, можно принять 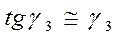.Тогда (4.51) приобретает вид

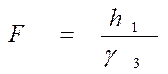. (4.52)

Подставляя для 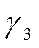его значение (4.50), получаем соотношение для оптической силы линзы

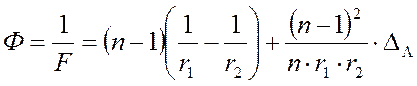. (4.53)

Оптическая сила линзы является одним из ее основных показателей.

Единицей оптической силы диоптрия (дптр.), которая равна оптической силе линзы, находящейся в вакууме, с фокусным расстоянием в 1 см.Оптическая сила 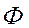является также мерой оптического действия системы, состоящей из комбинации линз. Расстояние от фокального пятна до вершины линзы

, (4.54)

а расстояние от вершины до главной плоскости Н – Н

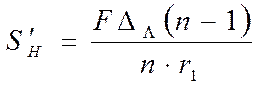. (4.55)

Для тонкой линзы, когда расстояние между вершинами поверхностей (толщина линзы) 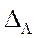значительно меньше величин радиусов кривизны 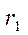и 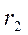принимается условие 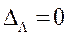, тогда формула (4.53) принимает вид

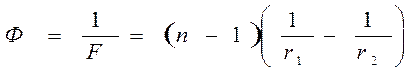. (4.56)

Эти же выражения можно использовать для расчета параметров отраженного светового луча от сферических зеркал. Но при этом надо изменить знак показателя преломления на противоположный, сохранив его абсолютное значение.

Аберрация

Важным понятием, необходимым для установления закономерностей прохождения излучения в оптических системах, является аберрация.

Под аберрацией понимают погрешность изображения в оптической системе, вызываемую отклонением луча от направления оптической системы. Поскольку лазерное излучение отличается высокой степенью монохроматичности при фокусировке лазерного излучения будут отсутствовать хроматические аберрации, возникающие вследствие зависимости показателя преломления от длины волны. Это позволяет в дальнейшем рассматривать лишь монохроматические аберрации. Различают следующие основные монохроматические аберрации: астигматизм, кома, дисторсия и сферическая аберрация. Астигматизм, кома и дисторсия являются аберрациями наклонного пучка лучей. При лазерной обработке в большинстве случаев фокусирующие системы располагают так, чтобы главная ось была перпендикулярна оси лазерного излучения. Тогда расчет сводится к определению только сферической аберрации. Рассмотрим понятие сферической аберрации на примере прохождения параллельного пучка через линзу. Для упрощения первая поверхность линзы представлена в виде плоской, и лучи проходят ее без преломления. Вторую поверхность (сферическую) они встречают с разными углами падения. Поэтому наиболее удаленные от оптической оси лучи преломляются сильнее остальных и сходятся за линзой в точке, которая расположена на самом большом расстоянии от фокальной плоскости. Это приводит к тому, что исходный цилиндрический пучок излучения после преломления линзой получает вид не конуса, а воронкообразной фигуры. Таким образом, точечное изображение в фокусе отсутствует.

Расстояние по оптической оси между точками схода параксиальных и крайних лучей 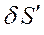называется продольной сферической аберрацией.

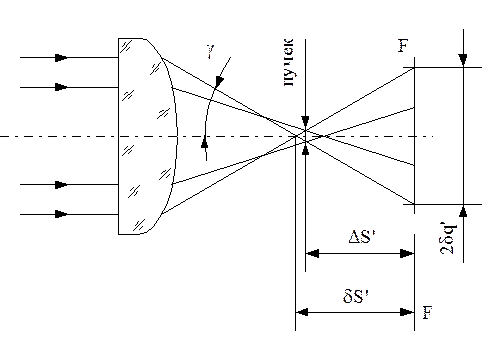
Рисунок 4.35 - Схема сферической аберрации

Радиус круга рассеяния в фокальной плоскости 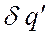называется поперечной сферической аберрацией.

Наименьший по площади круг рассеяния образуется на расстоянии 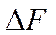от фокальной плоскости. Плоскость, соответствующая наименьшему кругу рассеяния, называется плоскостью наилучшей установки (ПНУ). Диаметр круга рассеяния в ПНУ ориентировочно составляет ½ величины поперечной сферической аберрации

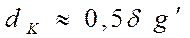, (4.57)

а расстояние от ПНУ до фокальной плоскости приближенно равно ¾ продольной сферической аберрации

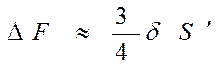. (4.58)

Точный расчет величины аберраций представляет достаточно сложную математическую задачу, которая решается в теории аберраций. Если учесть, что этот расчет приходится проводить несколько раз до получения требуемого результата, то понятно, что это дело специалистов математиков, оснащенных вычислительной техникой. Для инженерных расчетов из теории аберраций после каскада упрощающих допущений выводится формула

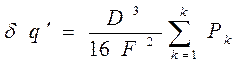, (4.59)

где 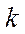- номер оптической поверхности;

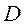- диаметр входного лазерного излучения;

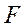- фокусное расстояние оптической системы.

Параметр 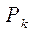вычисляется по формуле

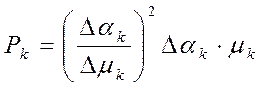. (4.60)

Здесь 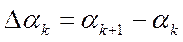, (4.61)

где 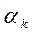- тангенс угла наклона крайнего периферийного лазерного луча после преломления на оптической поверхности, разделяющей k и k+1 области;

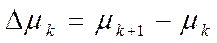, (4.62)

где 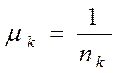- величина, обратная коэффициенту преломления.

Формула для расчета поперечной сферической аберрации хорошо работает в случае, когда лазерное излучение представляет собой параллельный пучок лучей, имеющий сечение круглой формы и главная плоскость фокусирующей системы перпендикулярна оси лазерного излучения , фокусирующая система тонкая, то есть можно принять 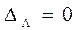. Диаметр фокального пятна в этом случае будет составлять

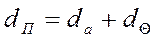, (4.63)

где 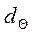- составляющая, обусловленная расходимостью луча, -

;

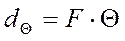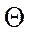- величина расходимости лазерного излучения;

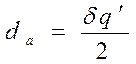- составляющая, обусловленная сферической аберрацией.