Частные решения уравнения диффузии
Из общих решений уравнения диффузии при D = const, приведённых в 5.3, могут быть получены частные решения для различных начальных и граничных условий.
1. Диффузия с постоянной поверхностной концентрацией (из неогра-ниченного источника). При постоянной концентрации на поверхностности в течение всего процесса диффузии (С(0, t) = Cs = const) и первоначальном отсутствии примеси в образце (C(x, 0) = 0) профиль распределения примеси выражается дополнительной функцией ошибок (рис. 5.4)
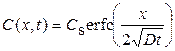 .
.
Количество примеси, продиффундировавшее в образец,
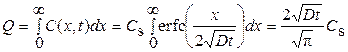 .
.
Описанные условия соответствуют первой стадии диффузии.
2. Диффузия из слоя конечной толщины. Исходная примесь первоначально находится в слое толщиной h, т. е. C(x, 0) = C0 при x ≤ h и
C(x, 0) = 0 при x > h, испарение с поверхности отсутствует (отражающая граница), 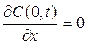 . В этом случае решение уравнения диффузии имеет вид (рис. 5.5)
. В этом случае решение уравнения диффузии имеет вид (рис. 5.5)
 |



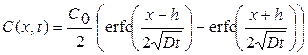
3. Диффузия из бесконечно тонкого слоя (из ограниченного источника).
Для бесконечно тонкого слоя при h → 0 из последнего выражения с учётом соотношения 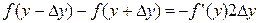 получаем
получаем
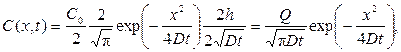
где Q – количество примеси в слое, Q = C0h.
4. Двухстадийная диффузия. Если эффективная толщина диффузион-ного слоя, сформированного на первой стадии h1 = 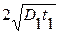 , значительно меньше толщины диффузионного слоя, сформированного на второй стадии h2 =
, значительно меньше толщины диффузионного слоя, сформированного на второй стадии h2 = 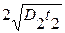 , или D1t1 << D2t2, тогда можно использовать выражение, полученное ранее для бесконечно тонкого слоя,
, или D1t1 << D2t2, тогда можно использовать выражение, полученное ранее для бесконечно тонкого слоя,
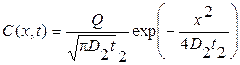 ,
,
где Q – количество примеси в слое, введённое во время первой стадии,
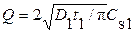 .
.
Здесь индекс 1 указывает на первую стадию, а индекс 2 – на вторую.
5. Многоэтапная диффузия. Под многоэтапной диффузией понимается диффузия в несколько этапов, на которых граничные условия не изменяются. В этом случае вид выражений для распределения примеси не изменяется, а произведение Dt заменяется на 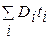 , где i – номер этапа; ti – длительность i-го этапа. Например, при двухэтапной диффузии из постоянного источника, когда концентрация на поверхности не меняется, С1(0, t) = С2(0, t) = Cs = = const,
, где i – номер этапа; ti – длительность i-го этапа. Например, при двухэтапной диффузии из постоянного источника, когда концентрация на поверхности не меняется, С1(0, t) = С2(0, t) = Cs = = const,
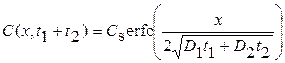 .
.
При двухэтапной диффузии из ограниченного источника, когда граница при x = 0 непроницаема 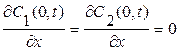 и количество примеси в слое не меняется, Q1 = Q2 = Q = const,
и количество примеси в слое не меняется, Q1 = Q2 = Q = const,
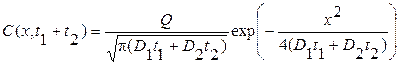 .
.
Дата добавления: 2016-12-16; просмотров: 1974;











