Уравнение диффузии и его общие решения

Уравнение диффузии выводится из первого закона Фика, который для одномерного случая имеет вид

,

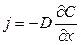где j – поток примеси, и условия непрерывности потока примеси в отсутствие объёмных стоков-истоков

.

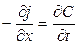В общем случае (при D ≠ const) одномерное уравнение диффузии имеет вид

.

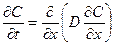Решение этого дифференциального уравнения в частных производных существует и единственно при наличии одного начального условия

C(x, 0) = C₀(x)

и двух граничных условий на границах области решения a ≤ x ≤ b для самой концентрации (граничные условия I рода)

C(a, t) = φ_a(t); C(b, t) = φ_b(t),

для её производной (граничные условия II рода)

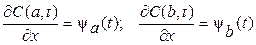
или для их линейной комбинации (граничные условия III рода).

В общем случае при D ≠ const уравнение диффузии не имеет простых аналитических решений и его необходимо решать численно. При постоянном коэффициенте диффузии D = const уравнение диффузии упрощается и принимает форму второго закона Фика

.

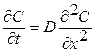Для неограниченного тела –∞ < x < ∞ при D = const уравнение диффузии имеет общее решение в интегральной форме:

.

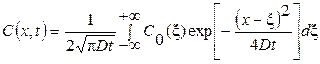Для полуограниченного тела (0 ≤ x < ∞) при D = const уравнение диффузии имеет общее решение в интегральной форме в виде

.

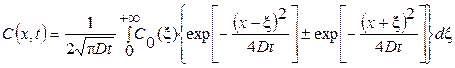Знак «+» между экспонентами в фигурных скобках соответствует граничному условию отражающей границы (отсутствие испарения) при x = 0 на поверхности 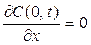, а знак «–» соответствует условию поглощающей границы (интенсивное испарение) C(0, t) = 0.