Плоскопараллельное движение механической системы
Ранее было показано, что плоское движение тела можно представить как геометрическую сумму двух движений: поступательного и вращательного. Поэтому, кинетическая энергия системы при ее плоском движении может быть найдена по формуле:

где Vc – скорость центра масс механической системы;
Icz – момент инерции механической системы относительно оси, проходящей через ее центр масс.
Найдем выражение, определяющее изменение величины кинетической энергии механической системы. Для этого докажем теорему об изменении кинетической энергии механической системы.
Рассмотрим механическую систему, состоящую из n материальных точек. Все силы, действующие на точки системы, разделим на внешние и внутренние. Таким образом, к каждой точке будут приложены по две сходящиеся системы сил: внешних и внутренних.
| Найдем равнодействующие этих систем: | 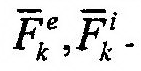
| внешних и внутренних сил, прило- |
женных к произвольной k-й точке механической системы соответственно. Тогда выражение (14.72) теоремы об изменении кинетической энергии k-й точки запишется в следующем виде:
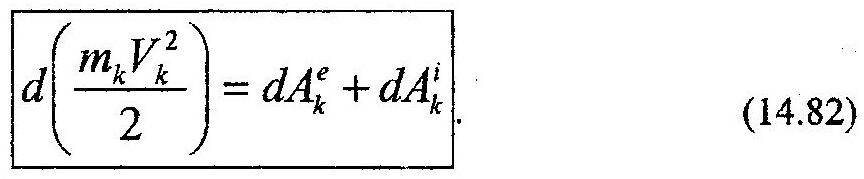
Очевидно, что такое же выражение можно записать для всех n точек системы. В результате получим систему n уравнений вида (14.82). Сложим почленно эти уравнения, получим:
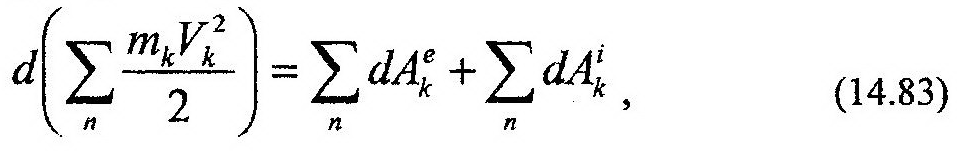
или:
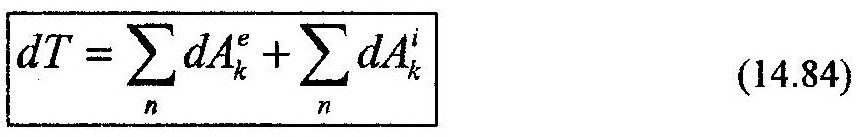
Выражение (14.84) отражает теорему об изменении кинетической энергии механической системы, записанную в дифференциальной форме.
Взяв интегралы от обеих частей (14.84), можно получить выражение этой же теоремы, записанное в интегральном виде:
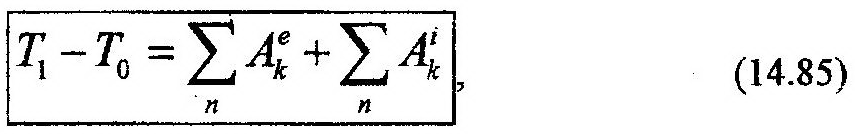
где Т0, Т1 – значения кинетической энергии системы в начальный и конечный моменты
времени,
т.е.: изменение кинетической энергии механической системы при некотором ее пере-
Дата добавления: 2016-12-16; просмотров: 2456;











