ЛЕКЦИЯ 10. Движение тела с одной неподвижной точкой
Примером такого движения является детский волчок. На рис. 9.10 показано тело, имею-
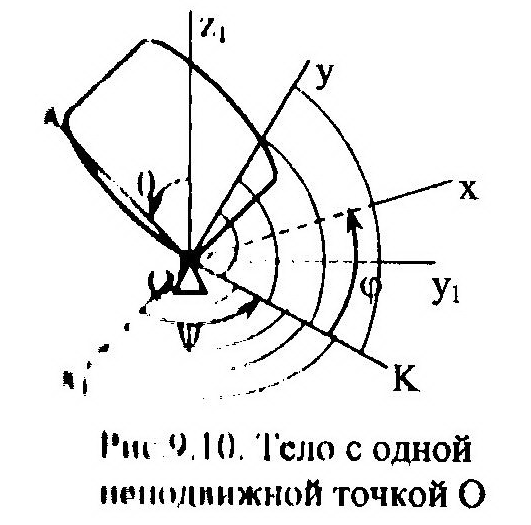
| щее единственную неподвижную точку О. Для установления параметров, определяющих положение такого тела в пространстве, используем две системы отсчета: неподвижную – x1y1z1 и подвижную, связанную с самим телом, - xyz. Начало отсчета для обеих систем свяжем с неподвижной точкой О. Прямую ОК, являющуюся результатом пересечения двух плоскостей: подвижной (хОу) и неподвижной (х1Оу1), называют линией узлов. Положение тела в пространстве можно однозначно определить с помощью трех углов: |
φ = ﮮКOх (угол собственного вращения),
ψ = ﮮ х1ОК (угол прецессии) и
θ = ﮮ z1Оz (угол нутации).
В таком случае, уравнениями движения тела будут зависимости вида:
По рис. 9.10 нетрудно представить, что изменение только угла φ приведет к вращению тела относительно оси Z. Если будет изменяться только угол ψ, то тело будет совершать прецессионное движение относительно оси Z1. Изменение только угла θ характеризует процесс нутации – углового перемещения тела относительно оси ОК. Тогда, из 7 осей (рис. 9.10) для описания движения тела достаточно только 3, это z, z1 и ОК.
Аналогично тому, как плоскопараллельное движение тела можно представить как непрерывная последовательность элементарных вращений относительно мгновенных центров скоростей, так и движение тела с одной неподвижной точкой можно рассматривать как последовательность элементарных поворотов вокруг мгновенных осей вращения. Это можно показать на основе теоремы Эйлера-Даламбера:
Дата добавления: 2016-12-16; просмотров: 1279;
Поиск по сайту
Узнать еще
- Cдвиг ветра. Воздействие на взлёт и посадку ВС. Рекомендации по выполнению полётов и управлению воздушным движением в условиях сдвига ветра.
- D-технология построения чертежа. Типовые объемные тела: призма, цилиндр, конус, сфера, тор, клин. Построение тел выдавливанием и вращением. Разрезы, сечения.
- I. Передвижение в основной стойке
- I.1.4 РАВНОМЕРНОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
- I.1.5 РАВНОПЕРЕМЕННОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
- I.1.7 ДВИЖЕНИЕ ТЕЛА ПО ОКРУЖНОСТИ
- I.3. Антитела системы АВ0
- I.6.3 ДВИЖЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ. УРАВНЕНИЕ БЕРНУЛЛИ
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
