Модель Лайдлера монетарного экономического цикла

Основоположником монетарной концепции экономических циклов считается Р. Хоутри. По его представлению, исходным пунктом экономического цикла является рост предложения кредита со стороны банковской системы. Далее следуют снижение ставки процента, рост инвестиций и совокупного спроса; так возникает фаза подъема, которая сопровождается ростом уровня цен. Со временем экономический подъем прекращается под воздействием двух основных факторов: внутреннего и внешнего. Первый сводится к исчерпанию избыточных резервов коммерческих банков; второй – к сокращению валютных резервов страны вследствие увеличения импорта и сокращения экспорта из-за повышения уровня цен. Оба названных фактора создают дефицит на рынке денег, и ставка процента начинает повышаться, а объем инвестиций – снижаться. Ухудшение инвестиционного климата на этой фазе развития цикла связано также с тем, что к концу фазы подъема разрыв между темпами роста уровня цен и ставки номинальной зарплаты сокращается. В результате начинаются обратные процессы: спад производства и занятости, снижение денежной ставки номинальной зарплаты и уровня цен, рост чистого экспорта, увеличение валютных резервов и денежной базы. Тем самым подготавливается основа для очередной кредитной экспансии банковской системы.

Рассмотрим более детально концепцию монетарного экономического цикла на примере модели Д. Лайдлера. Модель описывает взаимодействие рынков благ и денег в закрытой экономике без экономической активности государства. Для отображения динамики экономических параметров используются степенные функции.

Спрос на реальные кассовые остатки является функцией от реального дохода текущего периода: 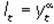. Предложение денег в каждом периоде задается экзогенно. Поэтому равновесие на денежном рынке выражается следующим равенством: .

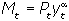В реальном секторе выпуск продукции зависит от степени использования существующих производственных мощностей, представленных национальным доходом полной занятости: 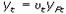, где - коэффициент использования производственных мощностей. Тогда условие равновесия на рынке денег будет 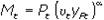, а равновесный темп роста предложения денег

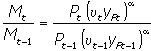
Для упрощения записи введем следующие обозначения:

.

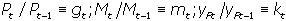Теперь уравнение равновесного темпа роста предложения денег принимает вид

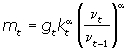
где g_t – темп ускорения роста уровня цен.

Изменение темпа роста предложения денег не нарушит равновесия на денежном рынке, если выполняется равенство

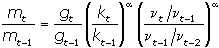
Уравнение описывает развитие экономической конъюнктуры в модели Лайдлера.

При динамическом равновесии темпы роста денежной массы и производственных мощностей постоянны 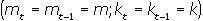и уравнение упрощается:

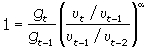
Как будет изменяться конъюнктура в экономике в случае отклонения от равновесного роста денежной массы, зависит от параметров уравнения, т.е. от изменений уровня цен (реакции монетарного сектора) и загрузки производственных мощностей (реакции реального сектора).

В рассматриваемой модели предполагается, что темп роста уровня цен определяется двумя факторами: степенью загрузки производственных мощностей (уровнем безработицы) и ожиданиями относительно роста уровня цен (g^e_t). Конкретно эта зависимость тоже выражается степенной функцией

.

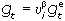где 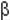– реакция занятости на повышение уровня цен ( > 1).

Соответственно темп ускорения роста уровня цен равен:

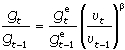
Для определения ожидаемой в текущем периоде величины роста уровня цен Лайдлер использует концепцию адаптивных ожиданий, в соответствии с которой существовавшее в предшествующем периоде предположение о степени роста уровня цен корректируется с учетом ошибки прогноза (разницы между фактическим и ожидавшимся ростом):

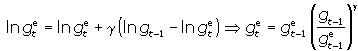
где γ – коэффициент корректировки ошибки прогноза.

Поэтому ожидаемый темп ускорения роста уровня цен равен:

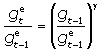
Поскольку в соответствии с уравнением 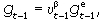то ожидаемый темп ускорения роста уровня цен в итоге определяется только степенью использования производственных мощностей:

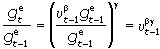
С учетом выражения темп фактического ускорения уровня цен (см. уравнение становится функцией от степени использования производственных мощностей в текущем и предшествующем периодах:

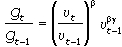
Теперь уравнение, определяющее характер развития экономической конъюнктуры в случае превышения равновесного темпа роста предложения денег, можно представить в следующем виде:

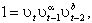
где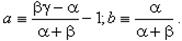

В результате логарифмирования степенного уравнения получается дифференциальное уравнение, подобное уравнению в модели Самуэльсона – Хикса:

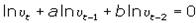
Равенство выполняется только при х_t = х_t-1 = х_t-2 = 1. Это значит, что динамическое равновесие достигается при полном использовании производственных мощностей. В этом случае, как следует из формулы, уровень цен растет с постоянным темпом, который в соответствии с уравнением равен 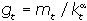. Поскольку в состоянии динамического равновесия k_t = const, то темп роста уровня цен прямо пропорционален темпу роста денежной массы. Иначе говоря, динамическое равновесие возможно при различных темпах инфляции лишь бы темп роста предложения денег соответствовал уравнению .

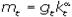Отклонение от равновесного темпа роста предложения денег нарушает динамическое равновесие в экономике. Перейдет ли после этого экономика к новому равновесному состоянию или нет, зависит от свойств этого дифференциального уравнения.

Динамическое равновесие в модели Лайдлера является устойчивым. В частности, это означает, что в долгосрочном периоде деньги нейтральны: после любого изменения их количества экономика вернется в равновесное состояние, но с другим темпом инфляции. В краткосрочном периоде изменение денежной массы отражается на степени загрузки производственных мощностей, уровне занятости и величине национального дохода.