Модель делового цикла Самуэльсона – Хикса

Экзогенная детерминистская теория цикла основывается на представлении о том, что колебания деловой активности обусловлены определенными факторами, которые, вызывая изменения основных экономических параметров, обеспечивают воспроизводство циклов. Ускорение или замедление развития экономики объясняется наличием временных лагов – систематических задержек в реакции на изменение условий экономической деятельности.

Так, согласно кейнсианским представлениям величина потребительских расходов C_t зависит от располагаемого дохода текущего периода Yd_t. Однако исследования, в частности, объяснявшие «загадку Кузнеца», показали, что более реалистичным является предположение о наличии связи между текущим потреблением и доходом предыдущего периода Yd_t-1. (лаг Робертсона).

Аналогично выявлена зависимость между текущим выпуском и совокупным спросом предыдущего периода (лаг Лундберга), поскольку фирмы при повышении совокупного спроса склонны сначала распродавать запасы, а только потом – расширять производство.

Указанные зависимости учитываются в модели мультипликатора-акселератора, предложенной П. Самуэльсоном иДж. Хиксом. Эта модель основывается на традиционных предпосылках кейнсианского анализа о неизменности цен и процентных ставок, когда объем выпуска определяется совокупным спросом. Изменения конъюнктуры оказывают влияние на инвестиции, которые посредством механизма мультипликатора влияют на совокупный выпуск (доход), вызывая его колебания, и как следствие – изменения в индуцированных инвестициях, увеличение (сокращение) которых стимулируется ростом (снижением) дохода – эффект акселератора. Таким образом, колебания совокупного выпуска объясняются взаимодействием мультипликатора и акселератора. Возврат к равновесию в данной модели определяется характером процесса – является он монотонным или колебательным.

Рассмотрим динамическую модель мультипликатора-акселератора с учетом лагов. Ее предпосылками являются, во-первых, использование в качестве объекта исследования закрытой двухсекторной экономики (т.е. без вмешательства государства); во-вторых, применение зависимости всех переменных от времени; в-третьих, стандартные предпосылки кейнсианского анализа рынка благ: жесткость цен, заработной платы и ставки процента.

Стандартная потребительская функция образуется с учетом зависимости объема потребительских расходов текущего периода от величины дохода предыдущего периода:

C_t = C_a + b∙Y_t-1, (2.1)

где С_а – автономный потребительский спрос;

b – предельная склонность к потреблению, 0 < b < 1.

Предприниматели осуществляют автономные инвестиции, объем которых при заданной ставке процента фиксирован, и индуцированные инвестиции, которые определяются приростом выпуска в предыдущие периоды (Y_t-1 – Y_t-2):

I_t = I_a + α∙(Y_t-1 – Y_t-2), (2.2)

где I_а – автономные инвестиции;

α – акселератор инвестиционных расходов.

Из условия равновесия на рынке товаров и услуг для открытой экономики получаем уравнение, характеризующее динамику выпуска во времени

Y_t = C_a + b∙Y_t-1 + I_a + α∙(Y_t-1 – Y_t-2) = (b + α) ∙Y_t-1 – α∙Y_t-2 + A_t, (2.3)

где А_t – все автономные компоненты совокупного спроса (А_t = С_а + I_а).

В долгосрочном периоде, если величина автономных расходов A_t остается неизменной в течение нескольких периодов, объем совокупного выпуска стабилизируется на некотором уровне Y^*: Y_t = Y_t-1 = Y_t-2 = ... = Y_t-n = Y^*.

Следовательно, равновесное значение дохода будет определяться следующим образом:

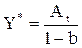. (2.4)

Величина 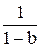представляет собой кейнсианский мультипликатор автономных расходов, показывающий изменение дохода в ответ на изменение каких-либо независимых компонентов совокупного спроса. Для того чтобы проследить динамику изменений выпуска, необходимо ввести следующее обозначение – отклонения фактического выпуска от его стабильного уровня:

∆Y_t = Y_t – Y^*. (2.5)

После подстановки выражения (2.5) в (2.3) получим

∆Y_t = (b + α) ∙∆Y_t-1 – α∙∆Y_t-2. (2.6)

Согласно теории решения дифференциальных уравнений динамика отклонения Y_t вследствие ΔY_t определяется значением дискриминанта характеристического уравнения, который будет равен D = (b + α)² – 4∙α. В зависимости от значения дискриминанта корни характеристического уравнения могут быть действительными (при D > 0 либо D = 0) или мнимыми (при D < 0). Если корни являются действительными, то процесс носит монотонный характер. При этом характер этого процесса определяется значением акселератора: если α < 1, то экономика, выведенная из равновесия, всегда будет к нему возвращаться, и процесс будет носить монотонный сходящийся характер. При значении акселератора, большем либо равном единице, процесс будет иметь монотонный расходящийся характер, т.е. экономика, выведенная из состояния равновесия, не сможет к нему вернуться.

Когда корни характеристического уравнения являются мнимыми, динамика отклонения фактического дохода от равновесного имеет колебательный характер. В зависимости от значения акселератора (меньше единицы, больше единицы или равен единице) характер колебаний может быть соответственно затухающим (рис. 2.1, а), расходящимся (рис. 2.1, б) или бесконечно повторяющимся с постоянной амплитудой (рис. 2.1, в).

Модель Самуэльсона – Хикса подтверждает возможность экономических колебаний и объясняет механизм воспроизводства этих колебаний с течением времени. при этом предполагалось, что восстановление равновесия происходит мгновенно и существующий объем избыточных производственных мощностей достаточен для полного удовлетворения эффективного спроса, возросшего в результате действия мультипликатора.

Хотя выводы данной модели имеют относительно слабую связь с эмпирическими наблюдениями, она заложила основы для других моделей деловых циклов. Несмотря на то, что в модели время учитывается в явном виде, она остается краткосрочной: приращение объема инвестиций, как и в статических моделях, увеличивает только совокупный спрос; воздействие инвестиций на совокупное предложение через вступление в строй новых производственных мощностей не учитывается; это ограничение снимается в моделях экономического роста.

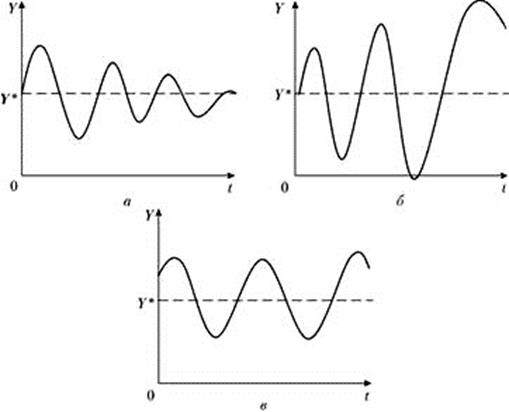
Рисунок 2.1 – Варианты колебаний выпуска в модели Самуэльсона – Хикса