Характеристика некоторых НЕ–факторов и методов их моделирования

Важной проблемой системного анализа является раскрытие неопределенностей, что обусловлено многообразием целей, свойств и особенностей исследуемых объектов.

Информационные технологии, являющиеся инструментом реализации методов системного анализа, в последние два десятилетия интенсивно развиваются в рамках научного направления, получившего название «инженерия знаний», основу которого составляют результаты разработок и исследований, связанные с искусственным интеллектом (ИИ): представление знаний и вывод на знаниях; системы искусственного интеллекта (экспертные системы, системы распознавания образов, системы поддержки принятия решений и др.).

Вместе с тем, различные предметные области, знания о которых могут быть положены в основу создания систем искусственного интеллекта, как правило, отрицают традиционные свойства формальных систем: точность, полноту, определенность, корректность, и др. Такие отрицаемые свойства были названы «НЕ–факторы», поскольку каждый из них лексически и содержательно фиксирует учет наших незнаний при абстрагировании, переходе к формальным системам и интерпретации выводов, полученных на формальном уровне. Поэтому любая формальная система всегда будет характеризоваться наличием определенных НЕ–факторов [12].

Данное обстоятельство полностью согласуется с основополагающим принципом неопределенности Вернера фон Гейзенберга и является отражением фундаментальной неопределенности процессов макромира.

В проблематике ИИ учет, анализ и управление НЕ–факторами имеет первостепенное значение, что обусловлено творческим характером задач создания интеллектуальных технологий, которые всегда решаются в условиях противоречивости, неполноты, неточности, неопределенности исходных данных, отношений между ними, операций их обработки (алгоритмов, процессов решения). Вместе с тем, как отмечают авторы работы [12], достаточно часто современные методы нечеткой математики, вероятностно-статистического вывода, байесовские и нейронные сети, генетические алгоритмы и др. используются без должного анализа природы присутствующих НЕ–факторов, что может привести к неадекватным моделям и выводам.

Первые НЕ–факторы, получившие название «нечеткость» или «неточность», были определены и изучались в рамках проблематики нечеткой математики, основателем которой является Лотфи Заде [16].

Однако, целенаправленные системные исследования НЕ–факторов начались с работ А.С. Нариньяни, в которых введено понятие и дана содержательная их трактовка [12, 28].

На рис. 1.5 представлена структура, характеризующая основные НЕ–факторы и методы их моделирования.

Неполнота. Некоторые данные не известны, но вся доступная информация полна и корректна. В приложении к проведению экспертизы такая ситуация может характеризоваться тем, что руководитель экспертизы предоставил экспертам инструкцию на формирование оценок не учитывающую всю полноту свойств, характеристик, параметров анализируемого объекта.

Единственным способом сокращения этого незнания является доработка инструкции в плане учета недостающих данных (пополнение информации).

Неопределённость. Доступная информация может быть истинной или ложной и оценивается с помощью вероятностных оценок. Например, при проведении анализа экспертных оценок руководителю экспертизы не была предоставлена информация о компетентности экспертов. Это порождает неопределенность относительно сформированных экспертных оценок, и степень доверия к ним со стороны руководителя экспертизы может быть выражена с помощью соответствующей вероятностной оценки.

Неточность (нечеткость). Имеется информация, достоверность которой не вызывает сомнений, однако она не точна. Например, информация полученная от экспертов достоверна, но вследствие того, что необоснованно были выбраны методы для её получения, она может быть неточной. Анализ такой информации выполняется методами нечеткой логики, нечётких множеств, нечетких отношений.

Однако, на практике могут быть ситуации в которых одновременно присутствуют различные формы незнания, например комбинация неопределенности и неточности.

Это обусловлено тем, что экспертные суждения относительно изучаемой проблемы могут взаимодействовать между собой (объединяться или пересекаться) в той или иной мере относительно той информации, которую они могут дать о множестве исходных данных (свойств, признаках, характеристиках) объекта или системы. Такие комбинации НЕ–факторов могут быть промоделированы методами теории свидетельств Демпстера–Шейфера и теории правдоподобных и парадоксальных рассуждений Дезера–Смарандаке [40, 41, 42].

Неупорядоченность. Достаточно часто возникают ситуации, когда данные или знания не являются точными и невозможно выполнить их точную классификацию (установить классификационную категорию). Например, пусть исходное множество элементов знаний Х представлено двумя классами: 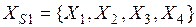и , , и 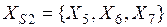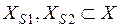пусть получено некоторое целевое подмножество знаний 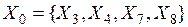, которое необходимо отнести к одному из указанных классов. Однако, можно видеть, что элементы 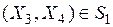, , 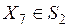а элемент 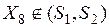. Это характеризует наличие своего рода «неточной» классификации, что на практике может выглядеть более реально, чем точная классификация. Для анализа таких ситуаций была предложена теория грубых множеств, позволяющая обрабатывать имплицитные массивы неупорядоченных данных и на основе такой обработки извлекать новые знания [36, 39, 42].

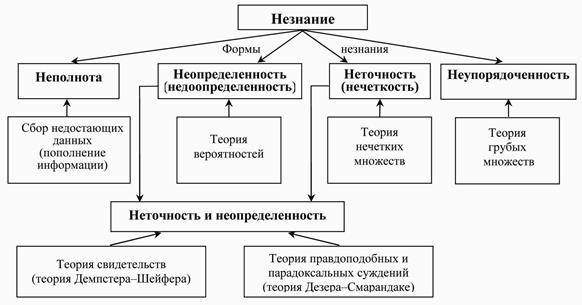
Рис. 1.6. Классификация форм незнания и методов их моделирования

Рассмотрим приведенные НЕ–факторы с позиции перечисленных теорий, что будет способствовать более четкому их различию.

Теория вероятностей оперирует с шансами случайных событий, при этом предполагается, что все события являются хорошо определёнными понятиями. Неопределённость здесь связана только с тем, с какими шансами может произойти каждое случайное событие из полной группы таких событий. Для этого необходимо выполнение двух условий: рассматриваются все возможные в данной ситуации события; реализоваться может только одно из событий.

Часто эти два условия формулируются следующим образом: полную группу событий образуют взаимно исключающие и исчерпывающие события. Традиционно вероятностные оценки p(e_i) случайных событий e_i, 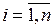подчиняются следующей системе аксиом:

1. ,

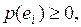
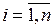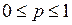
2. 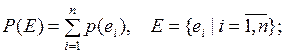(1.1)

3.

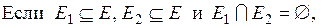
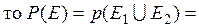
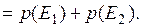
Аксиомы 2 и 3 свидетельствуют об аддитивном характере вероятностных оценок, т.е. в любом случае сумма вероятностей всех случайных событий, образующих полную группу, равна .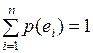

Следует указать на то, что существует два основных подхода к оцениванию вероятностей событий: объективные оценки вероятностей на основе метода частот и субъективные оценки вероятностей, источниками которых являются эксперты. В первом случае для моделирования неопределенностей могут быть использованы аналитические методы вероятностного вывода, вероятностный вывод на деревьях вероятностей, методы математической статистики, байесовские стратегии и др. Оценки второго вида могут быть использованы для вероятностного вывода на деревьях решений, на сетях уверенностей (сети Байеса), в задачах классификации (байесовские классификаторы), в задачах принятия решений в условиях риска и др.

Теория нечетких множеств предназначена для оперирования нечёткими концепциями, которые лежат в основе формирования множеств элементов. Предполагается, что элементы являются хорошо определёнными понятиями. Неопределённость (неточность, нечеткость) здесь возникает при попытке отнести элементы к некоторым классам (множествам), поскольку эти классы (множества) являются нечёткими, следовательно, плохо определенными.

Основным математическим аппаратом нечеткой (fuzzy) алгебры и нечеткой логики является лингвистическая переменная (ЛП), значения которой определяются набором вербальных (словесных) характеристик некоторого свойства объекта. Значения ЛП характеризуются так называемыми «нечеткими множествами» (НМ), которые в свою очередь определяются через некоторую базовую числовую шкалу А и функцию принадлежности μ_A(x), x Î A, μ_A(x) Î [0,1]. Таким образом, НМ – это совокупность пар вида (x, μ_A(x)), которая определяет субъективную степень уверенности в том, что данное конкретное значение А соответствует определенному элементу НМ.

Данная теория в качестве «инструментов» моделирования неточностей (нечеткостей) предоставляет методы построения функций принадлежности, формирования баз знаний, анализа нечетких отношений и др. Кроме этого, методы нечетких множеств и нечеткой логики могут быть использованы в задачах классификации, принятия решений, прогнозирования, а также при создании систем искусственного интеллекта, в которых используются сочетания возможностей нечеткой математики с нейронными сетями, генетическими алгоритмами и др.

Теория свидетельств Демпстера–Шейфера. Как уже отмечалось выше, теория вероятностей имеет дело с каждым отдельным событием (синглетоном) из полной группы событий и может корректно обращаться с неопределенностями, которые подчиняются аксиомам (1.1). Вместе с тем, в реальных условиях могут существовать и специфические формы НЕ–факторов, например, комбинация неопределенности и неточности (нечеткости), возникающие в процессе взаимодействия между суждениями экспертов. Формы таких взаимодействий могут иметь различный характер – они могут быть согласованными, совместимыми; могут произвольным образом объединятся и пересекаться. Для моделирования указанных форм взаимодействий может быть использована теория свидетельств Демпстера–Шейфера (ТДШ), основу которой составляют следующие положения.

Имеется множество элементов 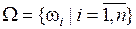, называемое основой анализа. Предполагается, что основа анализа Ω представляет собой множество исчерпывающих (всех возможных в данной ситуации) элементов и взаимно исключаемых (уникально определенных и отличных от других) элементов. При этом априори известно, что только единственный элемент ω₀ÎΩ является истинным в каждой конкретной ситуации. Этот элемент называется действительным миром.

На основе анализа Ω могут быть сформированы произвольные подмножества элементов A_i 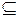Ω при предположениях (свидетельствах), что действительный мир ω₀ может принадлежать каждому из этих подмножеств.

Свидетельствами называют любые источники информации, на основании которых могут быть получены интересующие нас оценки степеней уверенности. Подмножества A_i могут принимать различные формы и взаимодействовать произвольным образом A_i = {ω₁} – единичное подмножество; A_j = {ω₂, ω₃, ω₄} – многоэлементное подмножество; A_i 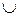A_j – объединение подмножеств A_i и A_j; A_i 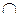A_j – пересечение подмножеств A_i и A_j, и др.

Подмножества A_i основы анализа Ω, которым эксперт назначил степени уверенности (основные массы вероятности m(A_i)) того, что действительный мир может находиться в любом из этих подмножеств, называют фокальными элементами.

Следует отметить, что m(A_i) определяет степень уверенности, отдаваемую A_i, но никаким подмножествам A_i. Это принципиальное положение теории свидетельств.

Наряду c назначениями масс вероятностей m(A_i) на подмножествах основы анализа Ω, концептуальную основу ТДШ составляют такие понятия как функция уверенности и функция правдоподобия.

Значения первой функции для отдельных подмножеств Ω выражают всю степень поддержки, отдаваемую каждому из таких подмножеств. Значения второй функции для каждого из подмножеств Ω выражает полную степень потенциальной поддержки, которая может быть отдана каждому из этих подмножеств.

Если на одной и той же основе анализа Ω назначения степеней уверенности (основных масс вероятности) выполняют несколько независимых экспертов, то возникает задача комбинирования этих назначений. Это производится на основе различных правил комбинирования свидетельств: Демпстера, Ягера, Инагаки, Дюбуа и Прада и др., которые могут быть использованы в ситуациях наличия специфических (комбинированных) НЕ–факторов.

Теория правдоподобных и парадоксальных рассуждений Дезера–Смарандаке (ТДС) может рассматриваться, как более углубленный вариант ТДШ в том плане, что она может оперировать с более сложными формами НЕ–знания. Например, если элементы основы анализа ω_i отражают нечеткие и неопределенные понятия: старость-молодость, цветовую гамму и т.д., то некоторые из элементов могут в значительной степени перекрываться друг другом, поэтому выделить полностью различающиеся ω_i не представляется возможным. В основе концепции ТДС лежат понятия свободной и гибридноймодели.

Свободная модель, обозначаемая М(Ω) рассматривает Ω только как основу исчерпывающих элементов 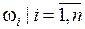, которые потенциально могут перекрываться. Гибридная модель определяется из свободной модели путем введения некоторых ограничений общности на некоторые подмножества элементов A_i из множества всех возможных подмножеств 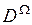, когда полагается, что A_i ≠ Ø. Это объясняется тем, что в реальных задачах нет необходимости назначать основные массы вероятностей всем возможным подмножествам 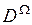, так как всегда возможны элементы, которые будут взаимно исключающими. В качестве ограничений общности широко применяются: ограничение исключаемости 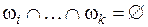и ограничение несуществования 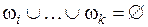. Так же, как и в теории свидетельств, в ТДС присутствует правило комбинирования, отражающее конъюнктивный консенсус между различными группами свидетельств. В заключение приведем ряд соображений, характеризующих различия между теорией вероятности, ТДШ и ТДС [42].

Пусть Ω= {ω₁,ω₂} – простейшая основа анализа, состоящая только из двух элементов. Тогда теория вероятностей имеет дело при предположении исключаемости гипотез с основными назначениями вероятностей, такими что m(ω₁)+m(ω₂)=1; ТДШ имеет дело при предположении исключаемости и исчерпываемости гипотез с основными назначениями уверенностей, такими что m(ω₁)+m(ω₂)+m(ω₁ 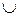ω₂)=1. ТДС имеет дело с единственным предположением исчерпываемости гипотез с обобщенными назначениями вероятностей, такими что m(ω₁)+m(ω₂)+m(ω₁ 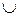ω₂)+ m(ω₁ 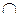ω₂)=1.

Теория грубых множеств (ТГМ). Методы, предложенные в рамках этой теории позволяют обрабатывать большие массивы неупорядоченных данных и на основе результатов такой обработки получать новые знания. Данная теория основана на том, что знания глубоко внедрены в способность людей выполнять классификацию предметов, явлений, объектов, ситуаций и др. Поэтому знания в теории грубых множеств обязательно связаны с множеством образцов классификации, относящихся к специфическим частям реального или абстрактного мира, называемого универсумом рассуждений (или, кратко, универсумом) [39, 42].

Фактически знания состоят из семейства различных образцов классификации интересующей предметной области.

База знаний в данной теории определяется как K=(U, R), где U – универсум и R – отношение эквивалентности, на основе которого могут быть выделены классы эквивалентности (категории) элементов U. В каждую категорию включаются элементы, которые обладают одинаковыми значениями классификационных признаков (атрибутов). Внутри каждой категории элементы считаются неразличимы.

Рассмотренные теории моделирования НЕ–факторов, несмотря на некоторые кажущиеся аналогии между ними, являются совершенно различными теориями. В основе каждой из них лежит специфический математический аппарат, и они предназначены для моделирования различных НЕ–факторов.

Сходство между этими теориями заключается лишь в способах получения исходной информации. Оценки вероятностей могут быть получены как объективным, так и субъективным (экспертным) путем. В теории нечетких множеств, для оценки степеней принадлежности элементов данному нечеткому множеству, также используются субъективные оценки. В ТДШ и ТДС для получения оценок степеней уверенности используют только субъективные подходы.

Что же касается ТГМ, то здесь классификация экспертных знаний (оценок) выполняется на основе отношений эквивалентности.

Рассмотренные теории были положены в основу целого ряда методов поддержки принятия решений, которые будут представлены ниже.