ПРАВИЛЬНАЯ ПИРАМИДА

Пирамида называется правильной, если ее основанием является правильный многоугольник, а основание высоты совпадает с центром многоугольника. Напомним, что центром правильного многоугольника является центр вписанной (описанной) окружности. Легко доказать (докажите самостоятельно), что у правильной пирамиды боковые ребра равны, следовательно, боковые грани – равные равнобедренные треугольники.

Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.

Боковой поверхностью пирамиды (точнее, площадью боковой поверхности) называется сумма площадей ее боковых граней.

Полная поверхность пирамиды (точнее, площадь полной поверхности) равна сумме боковой поверхности и площади основания.

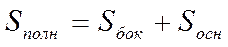
Теорема. Боковая поверхность правильной пирамиды равна произведению полупериметра основания на высоту боковой грани (l):

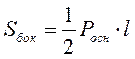
Доказательство:

Рассмотрим любую правильную пирамиду. Чтобы найти площадь боковой поверхности нужно сложить площади боковых граней пирамиды. Составим формулы для площадей всех треугольников (т.е.всех боковых граней):

, , ,…, .

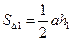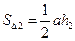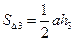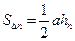Так как боковые грани правильной пирамиды – равные равнобедренные треугольники, то их высоты проведенные к основанию равны: 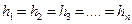, следовательно сумма площадей боковых граней равна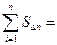

Объем любой пирамиды равен одной трети произведения площади ее основания на высоту.

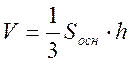
Что еще важно знать

Если боковые рёбра пирамиды с плоскостью основания образуют равные углы, то рёбра пирамиды равны, и вершина пирамиды проектируется в центр окружности, описанной около многоугольника основания (т.е. высота пирамиды падает в центр окружности, описанной около многоугольника основания).

У пирамиды могут быть равны боковые рёбра тогда, когда около многоугольника основания можно описать окружность.

Для таких пирамид нельзя использовать формулы правильной пирамиды для вычисления площади боковой поверхности, площадь боковой поверхности находят, сложив площади всех боковых граней пирамиды:

Ss=S1+S2+...

Главные зависимости для многоугольников, около которых можно описать окружность

Многоугольник, около которого можно описать окружность	Центр описанной окружности	Формулы
произвольный треугольник	точка пересечения серединных перпендикуляров	R=abc4S asinα=2R где a,b,c — стороны треугольника
равнобедренный треугольник	точка пересечения серединных перпендикуляров находится на высоте, проведенной к основанию	R=abc4S asinα=2R
прямоугольный треугольник	середина гипотенузы	R — половина гипотенузы
прямоугольник	точка пересечения диагоналей	R — половина диагонали

Если боковые грани пирамиды с её основанием образуют равные двугранные углы, то все высоты боковых граней пирамиды равны (у правильной пирамиды это апофемы), и вершина пирамиды проектируется в центр окружности, вписанной в многоугольник основания (высота пирамиды падает в центр окружности, вписанной в многоугольник основания).

У пирамиды могут быть равные двугранные углы при основании тогда, когда в многоугольник основания можно вписать окружность.

Для таких пирамид при вычислении площади боковой поверхности применяются формулы, которые используются для правильной пирамиды: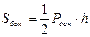

Главные зависимости для многоугольников, в которые можно вписать окружность

Многоугольник	Центр вписанной окр.	Формулы
любой треугольник	точка пересечения биссектрис	r=S_Δ·p, где p — полупериметр
ромб	точка пересечения диагоналей	r=Sромба·p r — половина высоты ромба

Отмечая радиус r на рисунке, нужно быть очень внимательным! Радиус вписанной окружности перпендикулярен стороне. Например, в произвольном треугольнике он не находится на биссектрисе и в ромбе не параллелен стороне.

Для вычисления площади боковой поверхности правильной пирамиды существует еще одна формула:

Sбок = Sоснования·cosϕ , где P — периметр основания, h — апофема, ϕ — двугранный угол при основании.