ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ 3 глава
5. Камень, брошенный горизонтально, упал на землю через 0,5 с на расстоянии 5 м по горизонтали от места бросания. Не учитывая сопротивления воздуха, определить: а) с какой высоты брошен камень? б) чему равна начальная скорость камня? в) с какой скоростью камень упал на землю? г) какой угол составляет траектория камня с горизонтом в точке его падения на землю?
6. Колесо радиусом 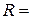 0,1 м вращается так, что зависимость угловой скорости от времени задается уравнением
0,1 м вращается так, что зависимость угловой скорости от времени задается уравнением 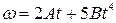 , где А=2 рад/с2 и В=1 рад/с5. Определить полное ускорение точек обода колеса через t=1 с после начала вращения и число оборотов, сделанных колесом за это время.
, где А=2 рад/с2 и В=1 рад/с5. Определить полное ускорение точек обода колеса через t=1 с после начала вращения и число оборотов, сделанных колесом за это время.
7. Частота вращения колеса при равнозамедленном движении за t=1 мин уменьшилась от 300 до 180 об/мин. Определить: а) угловое ускорение колеса; б) число полных оборотов, сделанных колесом за это время.
8. Диск радиусом R=10 см вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением 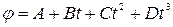 (В=1 рад/с, С=1 рад/с2, D=1 рад/с3). Определить для точек на ободе колеса к концу второй секунды после начала движения: а) тангенциальное ускорение; б) нормальное ускорение; в) полное ускорение.
(В=1 рад/с, С=1 рад/с2, D=1 рад/с3). Определить для точек на ободе колеса к концу второй секунды после начала движения: а) тангенциальное ускорение; б) нормальное ускорение; в) полное ускорение.
9. Колесо, вращаясь равноускоренно, достигло угловой скорости 20 рад/с через 10 оборотов после начала вращения. Найти угловое ускорение колеса.
10. Колесо, вращаясь равноускоренно, спустя 1 мин после начала движения приобретает скорость, соответствующую частоте 720 об/мин. Найти угловое ускорение колеса и число оборотов за эту минуту.
ГЛАВА 2. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
И ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
2.1. Первый закон Ньютона
Как уже отмечалось, динамика – это раздел классической механики, изучающий движение материальных тел под действием приложенных к ним сил, т.е. дающий связь между взаимодействиями тел и изменениями в их движении. Она является основным разделом механики и базируется на трех законах Ньютона (1687 г.)
Первый закон Ньютона (закон инерции) формулируется следующим образом: всякое тело (материальная точка) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние.
Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при отсутствии или взаимном уравновешивании внешних воздействий называется инертностью. Если на тело действует неуравновешенная система сил, то инертность сказывается в том, что изменение состояния покоя или движения тела происходит постепенно, а не мгновенно. При этом движение изменяется тем медленнее, чем больше инертность тела. Мерой инертности тела при поступательном движении является масса.
Первый закон Ньютона выполняется не во всякой системе отсчета. Системы, в которых он выполняется, называются инерциальными системами отсчета. Инерциальной системой отсчета является такая система, относительно которой свободная материальная точка, не подверженная воздействию других тел, движется равномерно и прямолинейно, или по инерции. Система отсчета, движущаяся по отношению к инерциальной системе отсчета с ускорением, является неинерциальной, и в ней не выполняются ни закон инерции, ни второй закон Ньютона, ни закон сохранения импульса.
Понятие «инерциальная система отсчета» является научной абстракцией. Реальная система отсчета всегда связывается с каким-нибудь конкретным телом (Землей, корпусом корабля и т.п.), по отношению к которому и изучается движение тех или иных объектов. Однако в природе нет неподвижных тел (тело, неподвижное относительно Земли, будет двигаться вместе с нею ускоренно по отношению к Солнцу и звездам), поэтому любая реальная система отсчета может рассматриваться как инерциальная лишь с той или иной степенью приближения. С очень высокой степенью точности инерциальной можно считать гелиоцентрическую (звездную) систему с началом координат в центре Солнца и с осями, направленными на три звезды. Для решения большинства технических задач инерциальной системой можно считать систему отсчета, жестко связанную с Землей (не учитывается вращение Земли вокруг собственной оси и вокруг Солнца).
Как уже отмечалось, масса – это физическая величина, определяющая инерционные свойства материи. Масса – это свойство самого тела и, в отличие от веса, не зависит от места ее измерения (вес Р тела в разных точках земного шара различен: он максимален на полюсах и минимален на экваторе). Ускорение свободного падения g тел на Землю также зависит от географической широты места наблюдения и от его высоты над уровнем моря. Однако отношение веса тела Р к его ускорению g одинаково во всех точках земного шара. Это отношение и принято для количественного измерения массы:
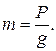 (2.1)
(2.1)
За единицу массы принят килограмм массы, равный массе эталона, сделанного из сплава иридия и платины. Следует отметить, что масса тела считается постоянной величиной только в классической механике Ньютона, изучающей движение тел со скоростями, небольшими по сравнению со скоростью света ( 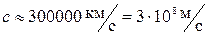 ). В современной физике установлено, что масса тела увеличивается с увеличением скорости его движения по закону:
). В современной физике установлено, что масса тела увеличивается с увеличением скорости его движения по закону:
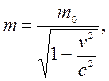
где m – масса тела, движущегося со скоростью 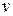 ; с – скорость света; m0 – масса покоящегося тела.
; с – скорость света; m0 – масса покоящегося тела.
Из формулы (2.1) следует, что вес тела
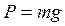 , (2.2)
, (2.2)
т.е. вес – это сила, с которой тело притягивается Землей, т.е. та сила, которая сообщает телу ускорение g=9,81 м/с2:
1 кГ=1 кг·9,81 м/с2 .
С другой стороны,
1 Н=1 кг·1 м/с2 ,
следовательно,
1 кГ=9,81 Н.
Для описания воздействий тел (материальных точек) друг на друга вводится понятие силы. Под действием сил тела либо изменяют скорость движения, т.е. приобретают ускорения (динамическое проявление сил), либо деформируются, т.е. изменяют свою форму и размеры (статическое проявление сил). Таким образом, сила - это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры. В каждый момент времени сила характеризуется числовым значением (модулем), направлением в пространстве и точкой приложения.
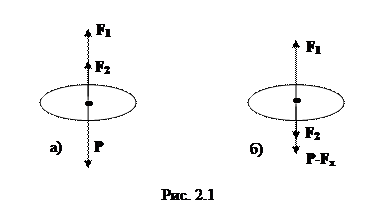
Пример. Какого веса балласт Fx надо сбросить с равномерно спускающегося аэростата, чтобы он начал подниматься с той же скоростью? Вес аэростата с балластом Р=1600 кГ, подъемная сила аэростата F1=1200 кГ. Силу сопротивления воздуха F2 считать одинаковой при подъеме и при спуске.
Решение
Так как движение равномерное, то по первому закону Ньютона равнодействующая сила равна нулю, т.е. 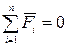 . При спуске аэростата (рис. 2.1, а) это уравнение принимает вид:
. При спуске аэростата (рис. 2.1, а) это уравнение принимает вид:
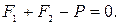
Когда балласт сброшен и аэростат начнет подниматься (рис. 2.1, б), получим уравнение следующего вида:
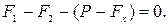
Решая оба уравнения совместно, найдем вес балласта:
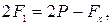
откуда 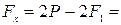 3200 кГ-2400 кГ=800 кГ=7,85·103 Н.
3200 кГ-2400 кГ=800 кГ=7,85·103 Н.
2.2. Второй закон Ньютона
Второй закон Ньютона – основной закон динамики поступательного движения – отвечает на вопрос, как изменяется механическое движение материального объекта (точки, тела) под действием приложенных к нему сил.
В динамике рассматриваются два типа задач, решения которых находятся на основе второго закона Ньютона. Задачи первого типа состоят в том, чтобы, зная движение тела, определить действующие на него силы. Классическим примером решения такой задачи является открытие Ньютоном закона всемирного тяготения: зная установленные Кеплером на основании результатов наблюдений законы движений планет, Ньютон доказал, что это движение происходит под действием силы, обратно пропорциональной квадрату расстояния между планетой и Солнцем.
Задачи второго типа являются в динамике основными и состоят в том, чтобы по действующим на тело силам определить закон его движения (уравнение движения). Для решения этих задач необходимо знать начальные условия, т.е. положение и скорость тела в момент начала его движения под действием заданных сил. Примерами таких задач являются следующие: а) по величине и направлению скорости снаряда в момент его вылета из канала ствола и действующим на снаряд при его движении силе тяжести и силе сопротивления воздуха найти закон движения снаряда, в частности его траекторию, горизонтальную дальность полета, время движения до цели; б) по известным скорости автомобиля в момент начала торможения и силе торможения найти время движения и путь до остановки.
Второй закон Ньютона формулируется следующим образом: ускорение, приобретаемое материальной точкой (телом), прямо пропорционально действующей силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела):
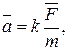 (2.3)
(2.3)
где 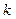 - коэффициент пропорциональности, зависящий от выбора системы единиц. В Международной системе (СИ)
- коэффициент пропорциональности, зависящий от выбора системы единиц. В Международной системе (СИ) 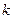 =1, поэтому
=1, поэтому
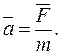 (2.4)
(2.4)
Второй закон Ньютона обычно записывается в следующей форме:
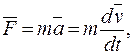
или
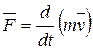 . (2.5)
. (2.5)
Вектор 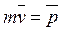 называется импульсом или количеством движения. В отличие от ускорения и скорости, импульс является характеристикой движущегося тела, отражающей не только кинематическую меру движения (скорость), но и его важнейшее динамическое свойство – массу.
называется импульсом или количеством движения. В отличие от ускорения и скорости, импульс является характеристикой движущегося тела, отражающей не только кинематическую меру движения (скорость), но и его важнейшее динамическое свойство – массу.
Таким образом, можно записать:
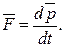 (2.6)
(2.6)
Выражение (2.6) является более общей формулировкой второго закона Ньютона: скорость изменения импульса материальной точки равна действующей на нее силе.
Это уравнение называется уравнением движения материальной точки.
Единица силы в системе СИ – ньютон (Н):
1 Н – это сила, которая телу массой в 1 кг сообщает ускорение 1 м/с2 в направлении действия силы:
1 Н = 1 кг·1 м/с2.
При действии на материальную точку нескольких сил справедлив принцип независимости действия сил: если на материальную точку действуют одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение, определяемое вторым законом Ньютона так, как если бы других сил не было:
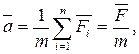
где сила 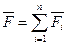 называется равнодействующей сил или результирующей силой.
называется равнодействующей сил или результирующей силой.
Таким образом, если на тело действует одновременно несколько сил, то, согласно принципу независимости действия сил, под силой 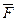 во втором законе Ньютона понимают результирующую силу.
во втором законе Ньютона понимают результирующую силу.
Второй закон Ньютона справедлив только в инерциальных системах отсчета. Первый закон Ньютона можно получить из второго закона: в случае равенства нулю равнодействующей силы ускорение также равно нулю, т.е. тело находится в покое или движется равномерно.
2.3. Третий закон Ньютона
Воздействие тел (материальных точек) друг на друга всегда является взаимным и определяется третьим законом Ньютона (законом о равенстве действия и противодействия): действия двух тел друг на друга всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти тела:
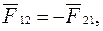 (2.7)
(2.7)
где 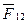 - сила, действующая на первое тело со стороны второго;
- сила, действующая на первое тело со стороны второго; 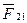 - сила, действующая на второе тело со стороны первого.
- сила, действующая на второе тело со стороны первого.
Необходимо помнить, что силы 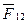 и
и 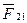 приложены к разным телам (материальным точкам) и поэтому не уравновешивают друг друга; они действуют парами и являются силами одной природы.
приложены к разным телам (материальным точкам) и поэтому не уравновешивают друг друга; они действуют парами и являются силами одной природы.
Примеры, иллюстрирующие третий закон Ньютона:
1) Человек прыгает с лодки на берег. Он толкает лодку назад с силой 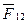 , а сам испытывает со стороны лодки силу
, а сам испытывает со стороны лодки силу 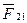 , направленную в сторону, противоположную направлению
, направленную в сторону, противоположную направлению 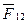 . Поэтому человек и лодка движутся в прямо противоположных направлениях.
. Поэтому человек и лодка движутся в прямо противоположных направлениях.
2) Камень массой m падает с обрыва на Землю с ускорением g. Он притягивается к Земле с такой же по величине силой, что и Земля к камню. Просто мы не замечаем движения Земли, т.к. ее масса М во много раз превышает массу m камня, следовательно, ускорение 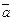 , с которым движется Земля, ничтожно мало по сравнению с ускорением g. В самом деле, с учетом второго закона Ньютона уравнение (2.7) запишется в виде:
, с которым движется Земля, ничтожно мало по сравнению с ускорением g. В самом деле, с учетом второго закона Ньютона уравнение (2.7) запишется в виде:
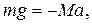
откуда
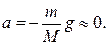
Заменим в уравнении (2.7) силы 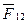 и
и 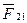 согласно формуле (2.5):
согласно формуле (2.5):
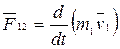 ;
; 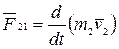 .
.
Тогда
 ,
,
или
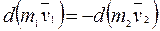 . (2.8)
. (2.8)
Следовательно, при механическом взаимодействии двух тел изменения их импульсов численно равно и противоположны по направлению.
Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками.
2.4. Закон сохранения импульса
Из второго и третьего законов Ньютона вытекает закон сохранения импульса замкнутой системы.
Совокупность материальных точек (тел), рассматриваемых как единое целое, называется механической системой. Силы взаимодействия между материальными точками механической системы называются внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют внешние силы (они взаимно уравновешиваются), называется замкнутой или изолированной. В такой системе необходимо учитывать только силы взаимодействия между входящими в нее телами (внутренние силы). Строго говоря, изолированных механических систем в природе не существует.
Рассмотрим изолированную механическую систему, состоящую из n тел с массами m1, m2,…, mn. Обозначим скорости этих тел через 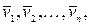 а внутреннюю силу, действующую на i-е тело со стороны k-го, - через
а внутреннюю силу, действующую на i-е тело со стороны k-го, - через 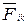 .
.
На основании второго закона Ньютона можно составить следующую систему уравнений движения всех тел системы:
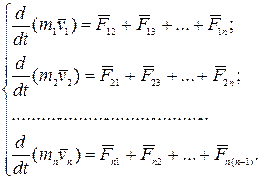
Складывая почленно эти уравнения и группируя силы 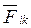 и
и 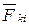 , получим:
, получим:
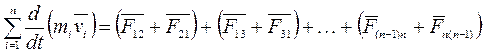 .
.
Согласно третьему закону Ньютона 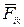 =-
=- 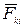 , поэтому все скобки в правой части этого уравнения равны нулю, т.е.
, поэтому все скобки в правой части этого уравнения равны нулю, т.е.
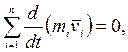 или
или 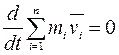 .
.
Векторная сумма 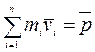 представляет собой импульс всей системы. Таким образом,
представляет собой импульс всей системы. Таким образом, 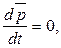 или
или
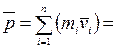 const. (2.9)
const. (2.9)
Выражение (2.9) представляет собой закон сохранения импульса: импульс замкнутой системы тел с течением времени не изменяется.
Закон сохранения импульса справедлив не только в классической механике; он выполняется и для замкнутых систем микрочастиц, т.е. действует и в квантовой механике. Другими словами, этот закон носит универсальный характер и является фундаментальным законом природы.
Закон сохранения импульса является следствием однородности пространства: при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства и законы движения не изменяются, т.е. не зависят от выбора положения начала координат инерциальной системы отсчета.
В классической механике из-за независимости массы от скорости импульс системы можно выразить через скорость ее центра масс.
Скорость i-й материальной точки связана с ее радиусом-вектором 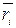 соотношением:
соотношением:
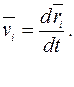
Следовательно,
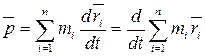 .
.
Центром масс или центром инерции системы материальных точек называется воображаемая тоска С, положение которой характеризует распределение массы этой системы. Ее радиус-вектор равен
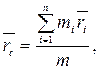
где 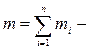 масса системы.
масса системы.
Скорость центра масс определяется выражением:
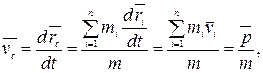
т.е.
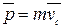 . (2.10)
. (2.10)
Другими словами, импульс системы равен произведению массы системы на скорость ее центра инерции.
Подставив выражение (2.10) в (2.9), получим:
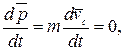
т.е. в изолированной механической системе центр масс находится в покое или движется равномерно и прямолинейно.
Если система незамкнутая (на нее действуют помимо внутренних и внешние силы), то выражение (2.9) с учетом (2.10) запишется следующим образом:
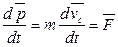 ,
,
или
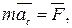 (2.11)
(2.11)
где 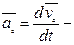 ускорение центра масс.
ускорение центра масс.
Из (2.11) вытекает закон (теорема) движения центра масс: центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, приложенных к системе.
2.5. Уравнение движения тела переменной массы
Получим уравнение движения тела переменной массы (например, движение ракеты сопровождается уменьшением ее массы за счет истечения газов, образующихся от сгорания топлива).
Пусть в момент времени t масса ракеты m, а ее скорость 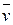 ; тогда по истечении времени dt ее масса уменьшится на dm и станет равной m–dm, а скорость увеличится до величины
; тогда по истечении времени dt ее масса уменьшится на dm и станет равной m–dm, а скорость увеличится до величины 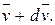 Изменение импульса системы за время dt будет равно:
Изменение импульса системы за время dt будет равно:
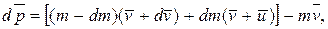
где 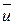 - скорость истечения газов относительно ракеты. Раскрывая скобки в этом выражении, получим:
- скорость истечения газов относительно ракеты. Раскрывая скобки в этом выражении, получим:
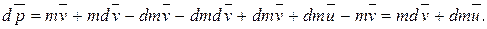
Если на систему действуют внешние силы, то 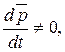 т.е.
т.е. 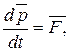 или
или 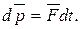 Тогда
Тогда 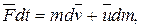 или
или
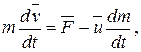 (2.12)
(2.12)
где член 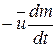 называют реактивной силой
называют реактивной силой 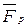 . Если вектор
. Если вектор 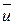 противоположен
противоположен 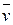 , то ракета ускоряется, а если совпадает с
, то ракета ускоряется, а если совпадает с 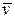 , то тормозится.
, то тормозится.
Таким образом, уравнение движения тела переменной массы имеет следующий вид:
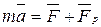 (2.13)
(2.13)
Уравнение (2.13) называется уравнением И.В. Мещерского.
Применим уравнение (2.12) к движению ракеты, на которую не действуют никакие внешние силы. Тогда, полагая 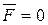 и считая, что ракета движется прямолинейно (скорость истечения газов постоянна), получим:
и считая, что ракета движется прямолинейно (скорость истечения газов постоянна), получим:
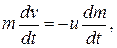
откуда
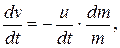
или
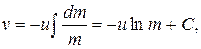
где С – постоянная интегрирования, определяемая из начальных условий. Если в начальный момент времени 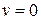 , а стартовая масса ракеты составляет m0, то
, а стартовая масса ракеты составляет m0, то 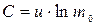 .Следовательно,
.Следовательно,
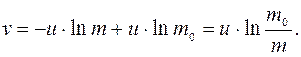 (2.14)
(2.14)
Полученное соотношение называют формулой К.Э. Циолковского. Из выражения (2.14) следуют следующие практические выводы:
а) чем больше конечная масса ракеты m, тем больше должна быть стартовая масса m0;
б) чем больше скорость истечения газов u, тем больше может быть конечная масса при данной стартовой массе ракеты.
Уравнения Мещерского и Циолковского справедливы для случаев, когда скорости 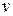 и
и 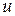 намного меньше скорости света с.
намного меньше скорости света с.
Краткие выводы
· Динамика – раздел механики, предметом изучения которого являются законы движения тел и причины, которые вызывают или изменяют это движение.
· В основе динамики материальной точки и поступательного движения твердого тела лежат законы Ньютона. Первый закон Ньютона утверждает существование инерциальных систем отсчета и формулируется следующим образом: существуют такие системы отсчета, относительно которых поступательно движущиеся тела сохраняют свою скорость постоянной, если на них не действуют другие тела или действие других тел компенсируется.
· Инерциальной называется система отсчета, относительно которой свободная материальная точка, на которую не действуют другие тела, движется равномерно и прямолинейно, или по инерции. Система отсчета, движущаяся относительно инерциальной системы отсчета с ускорением, называется неинерциальной.
· Свойство любого тела оказывать сопротивление изменению его скорости называется инертностью. Мерой инертности тела при его поступательном движении является масса.
· Сила – это векторная физическая величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры.
· Второй закон Ньютонаформулируется следующим образом: ускорение, приобретаемое телом (материальной точкой), пропорционально равнодействующей приложенных сил, совпадает с ней по направлению и обратно пропорционально массе тела:
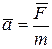 , или
, или 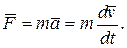
Более общая формулировка второго закона Ньютона гласит: скорость изменения импульса тела (материальной точки) равна равнодействующей приложенных сил:
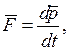
где 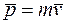 - импульс тела. Второй закон Ньютона справедлив только в инерциальных системах отсчета.
- импульс тела. Второй закон Ньютона справедлив только в инерциальных системах отсчета.
· Всякое действие материальных точек (тел) друг на друга взаимно. Силы, с которыми действуют друг на друга материальные точки, равны по модулю, противоположно направлены и действуют вдоль соединяющей точки прямой (третий закон Ньютона):
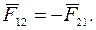
Эти силы приложены к разным точкам, действуют парами и являются силами одной природы.
· В замкнутой механической системе выполняется фундаментальный закон природы – закон сохранения импульса: импульс замкнутой системы материальных точек (тел) с течением времени не изменяется:
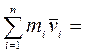 const,
const,
где n – число материальных точек в системе. Замкнутой (изолированной) называется механическая система, на которую не действуют внешние силы.
· Закон сохранения импульса является следствием однородности пространства: при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства не изменяются.
Вопросы для самоконтроля и повторения
1. Какие системы отсчета называются инерциальными? Почему система отсчета, связанная с Землей, строго говоря, неинерциальна?
2. Какое свойство тела называется инертностью? Что является мерой инертности тела при его поступательном движении?
3. Что такое сила, чем она характеризуется?
4. Какие основные задачи решает ньютоновская динамика?
5. Сформулируйте законы Ньютона. Является ли первый закон Ньютона следствием второго закона?
6. В чем заключается принцип независимости действия сил?
Дата добавления: 2016-12-16; просмотров: 1310;










