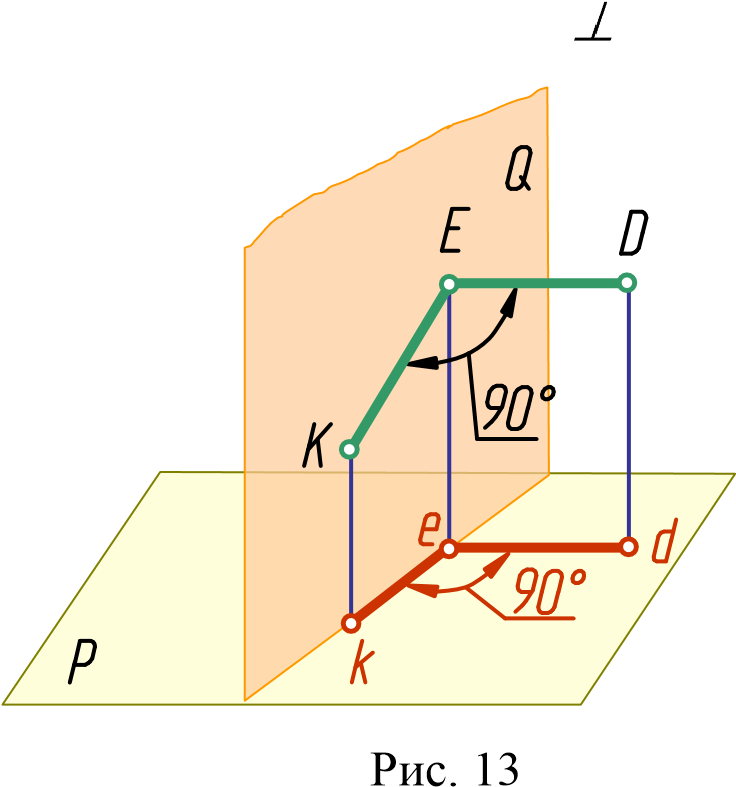
Теорема о проецировании прямого угла

Прямой угол проецируется в виде прямого угла, если одна из его сторон параллельна плоскости проекций, а вторая ей не перпендикулярна.

Пусть сторона DЕ прямого угла KED параллельна плоскости P, а сторона EK ей не перпендикулярна (рис. 13). Требуется доказать, что его проекция – угол ked – равна 90

Доказательство.Спроецируем стороны угла KED на плоскость Р. Для этого проведем проецирующие лучи из точек K, E, D перпендикулярно плоскости. Через прямые EK и Ee проведем дополнительную плоскость Q. Плоскость Q перпендикулярна плоскости P, так как она проходит через прямую Ee, перпендикулярную плоскости P.

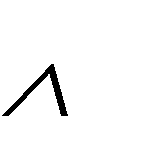
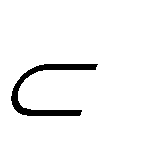
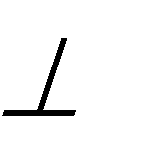
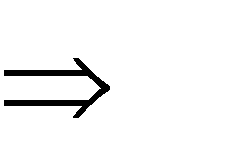
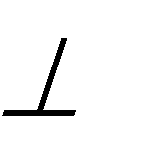(EK) (Ee) Q; (Ee) Р Q Р

Прямая ED перпендикулярна плоскости Q, так как она перпендикулярна к двум прямым этой плоскости EK и Ee.

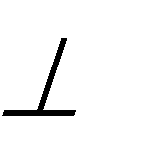
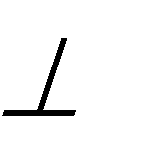
(ED) (EK); (ED) (Ee) (ED) Q

Прямая ed также перпендикулярна к плоскости Q, так как прямая ED и ее проекция ed параллельны между собой.

(ED) Q; (ed) // (ED) (ed) Q

Прямая ed перпендикулярна любой прямой, лежащей в этой плоскости, в том числе и прямой ek, то есть угол ked прямой.

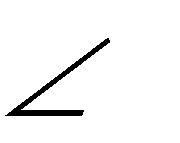
(ed) (ek); ked = 90.