Две основные задачи преобразования прямой

 Прямую общего положения можно преобразовать в: прямую уровня; проецирующую прямую.
Прямую общего положения можно преобразовать в: прямую уровня; проецирующую прямую.
1 Преобразование прямой общего положения в прямую уровня
Такое преобразование позволяет определить натуральную величину отрезка прямой и углы наклона его к плоскостям проекций.
При решении задачи новую плоскость, например, V1(рис. 5), ставим в положение, параллельное отрезку. В этом случае новая ось проекций будет проходить параллельно горизонтальной проекции прямой:
V V1

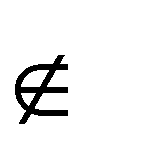 H H ; V1 H; V1 // AB; x1 // ab.
H H ; V1 H; V1 // AB; x1 // ab.


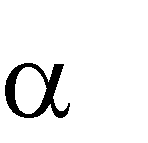 Через горизонтальные проекции a и b, перпендикулярно новой оси x1, проводим линии связи и на них откладываем z координаты точек (то есть расстояние от оси x до фронтальных проекций точек). Новая проекция a 1b 1 будет равна натуральной величине отрезка, а угол равен углу наклона отрезка к плоскости H.
Через горизонтальные проекции a и b, перпендикулярно новой оси x1, проводим линии связи и на них откладываем z координаты точек (то есть расстояние от оси x до фронтальных проекций точек). Новая проекция a 1b 1 будет равна натуральной величине отрезка, а угол равен углу наклона отрезка к плоскости H.
Преобразование прямой уровня в проецирующую прямую
В данном случае прямую необходимо поставить в положение, перпендикулярное плоскости проекций, чтобы на эту плоскость прямая спроецировалась в точку (рис. 6).
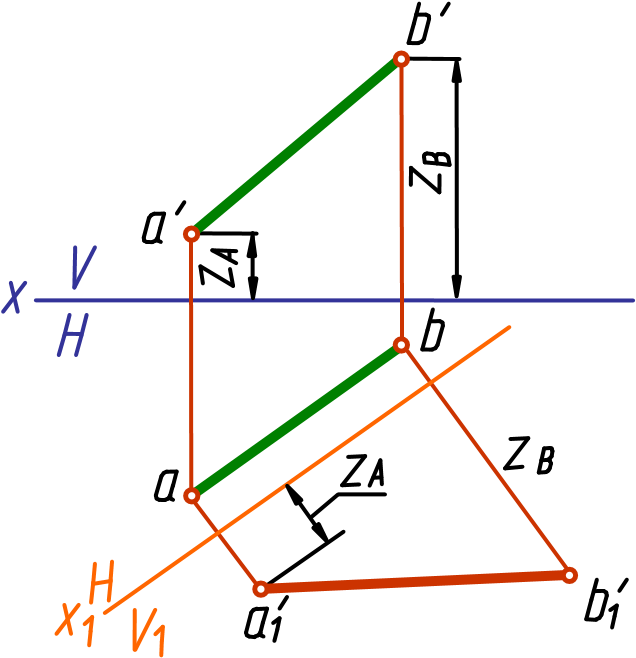
Рис. 5 Рис. 6


 Так как данная прямая параллельна горизонтальной плоскости проекций, то для преобразования ее в проецирующую прямую, необходимо заменить фронтальную плоскость V на новую V1. Располагаем плоскость V1 перпендикулярноAB. Тогда на плоскость V1 прямая спроецируется в точку (a 1=b 1).
Так как данная прямая параллельна горизонтальной плоскости проекций, то для преобразования ее в проецирующую прямую, необходимо заменить фронтальную плоскость V на новую V1. Располагаем плоскость V1 перпендикулярноAB. Тогда на плоскость V1 прямая спроецируется в точку (a 1=b 1).
V V1
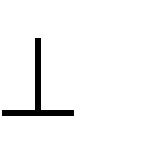
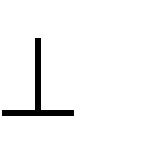
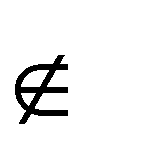 H H ; V1 H; V1 AB; x1 ab.
H H ; V1 H; V1 AB; x1 ab.
2. Преобразование прямой общего положения в проецирующую прямую
 Преобразовать прямую общего положения в проецирующую прямую за одну замену нельзя, так как невозможно расположить новую плоскость одновременно перпендикулярно прямой общего положения и оставшейся старой плоскости проекций.
Преобразовать прямую общего положения в проецирующую прямую за одну замену нельзя, так как невозможно расположить новую плоскость одновременно перпендикулярно прямой общего положения и оставшейся старой плоскости проекций.
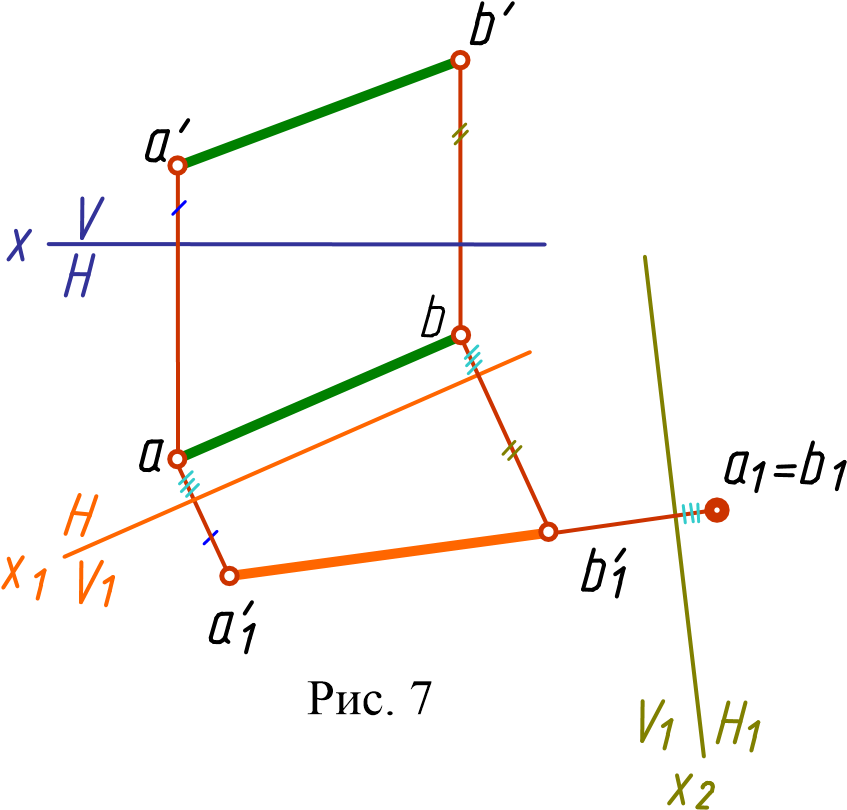
Чтобы прямую общего положения AB (рис. 7) преобразовать в проецирующую, проводят две замены, то есть обе задачи, первую и вторую, решают последовательно. Сначала прямую общего положения преобразуют в прямую, параллельную плоскости проекций (прямую уровня), а затем эту прямую преобразуют в проецирующую.
1. 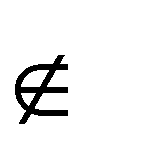
| H |
| V |
| H |
| V |
| 1 |

| 1 |
| H |
| V |
 ; V1 H; V1// AB; x1//ab;
; V1 H; V1// AB; x1//ab;
2. 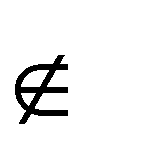
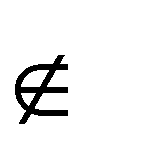
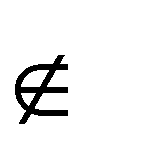

 V; H1 V1; H1 AB; x2 a 1b 1
V; H1 V1; H1 AB; x2 a 1b 1
H 1
Дата добавления: 2021-03-18; просмотров: 591;











