Статистическая интерпретация понятия энтропии

Макроскопическое состояние включает в себя множество микроскопических состояний. Их число для различных систем может подсчитываться по-разному. По Больцману макроскопическое состояние определяется количеством частиц на каждом энергетическом уровне. Частицы имеют свой номер, а полная энергия системы постоянна. Микроскопические состояния отличаются друг от друга распределением частиц по уровням энергий. Например, система из трех молекул, которые располагаются на трёх энергетических уровнях, а полная энергия системы равна пяти условным единицам, описывается двумя макроскопическими состояниями:

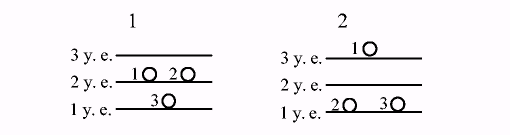
Каждому из них соответствуют по три микроскопических состояния (W₁=3, W₂=3):

W = = 3

В термодинамике мы имеем дело с системами, состоящими из огромного числа частиц, с множеством макросостояний с различными W.

Больцман вывел соотношение, связывающее абсолютную энтропию с числом микроскопических состояний системы, соответствующих данному макроскопическому состоянию (или термодинамической вероятностью):

S = k·1пW,

Где k =R/N_A = 1,38 • 10²³Дж • К ^-1 — постоянная Больцмана, а W— число микроскопических состояний системы.

Из формулировки второго начала термодинамики следует, что в изолированной системе при самопроизвольном процессе энтропия возрастает. Система будет самопроизвольно стремиться к макросостоянию с максимальным W. Отсюда энтропию можно рассматривать как меру хаоса системы.

При абсолютной температуре Т = 0⁰ К чистые химические вещества образуют идеальные кристаллы, и их состояние можно описать только одним способом (W = 1), а логарифм единицы равен нулю, а значит и энтропия при этой температуре равна нулю. Пользуясь этим, можно сформулировать третье начало термодинамики как: