Смешанные системы счисления

Неудобство использования двоичной системы счисления из-за громоздкости записи чисел, особенно при разработке программ на машинном языке, привели к использованию восьмеричной и шестнадцатеричной систем счисления.

В восьмеричной системе счисления базовыми цифрами являются:

0, 1, 2, 3, 4, 5, 6, 7.

А запись любого числа в этой системе основывается на его разложении по степеням числа восемь с коэффициентами из базовых цифр. Например, число 8310 десятичной системы можно представить следующим образом:

8310 =6410+1610+310= 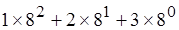= 1238

В шестнадцатеричной системе счисления базисными являются цифры от 0 до 15. В этой системе для обозначения всех базисных цифр не хватает цифр десятеричной системы, поэтому для обозначения первых десяти цифр используют цифры десятичной системы от 0 до 9, а для обозначения последующих шести цифр используют буквы:

10 – a, 11 – b, 12 – c, 13 – d, 14 – e, 15 – f.

Поэтому, например, число десятичной системы 175,510 в шестнадцатеричной системе имеет вид:

175,510= 16010 + 1510+ 810/1610= 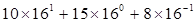= af,816

В ряде случаев, числа, заданные в одной системе счисления приходится изображать с помощью цифр другой системы счисления. Например, десятичные числа, с которыми мы привыкли работать, необходимо переводить в двоичные, с которыми должна работать ЭВМ. В этих случаях используются смешанные системы счисления, в которых каждый коэффициент Р-ичного разложения числа записывается в Q-ичной системе.

В такой системе Р называется старшим основанием, а Q - младшим основанием, а сама система счисления называется Q-Р-ичной..

Для того, чтобы запись числа в смешанной системе счисления была однозначной, на представление любой Р-ичной цифры отводится одно и то же количество Q-ичных разрядов, достаточное для представления максимального числа Р-ичной системы.

Так, для изображения числа в двоично-десятичной системе необходимо отвести четыре двоичных разряда потому, что максимальная цифра десятичной системы 910 отображается числом двоичной системы 10012, состоящей из четырех двоичных разрядов. Так например, число 19510 десятичной системы запишется в двоично-десятичной системе в виде:

0001 1001 01012-10 ,

где последовательные тетраэды (четверки) двоичных чисел изображают цифры 1, 9, 5, записи числа в десятичной системе счисления.

При решении задач с помощью ЭВМ исходные данные задаются обычно в десятичной системе, полученные решения также представляются в десятичной системе, а непосредственно в машине они могут обрабатываться в двоичной или восьмеричной, или в другой системе счисления.

Таким образом, возникает необходимость перевода чисел из одной системы в другую.