Методы измерения информации

Как и любое физическое вещество информация имеет свои количественные характеристики. В современной информатике приняты следующие методы измерения информации:

- объемный;

- энтропийный;

- алгоритмический.

Объемный метод измерения характеризуется количеством символов, содержащихся в конкретном сообщении. В вычислительной технике вся информация, независимо от ее природы (текст, число, изображение и т.д.), представляется в двоичной форме записи, т.е. состоящей из различных комбинаций двух символов 0 и 1. Один такой символ в вычислительной технике называется битом, совокупность восьми таких символов называется байтом, а большое количество символов, которыми оперирует ЭВМ, называется словом.

Энтропийный метод измерения информации используется в теории информации и кодирования. Он основывается на мере неопределенности появления некоторой совокупности событий и выражается вероятностью появления этих событий. Количество информации в сообщении при энтропийном методе оценки определяется тем, насколько уменьшается эта мера после получения сообщения. В теории информации используется следующая количественная мера:

Э = log₂ m,

где Э – энтропия;

m – число возможных равновероятных событий.

В случае, когда энтропия зависит не только от числа равновероятных событий выбора, но и от вероятности возможного выбора элемента информации К. Шеннон предложил следующую форму оценки энтропии:

Э = log₂ (1/Р_i) = - log₂ Р_i ,

где Р_i – вероятность возможного выбора i-го элемента информации.

Тогда среднее количество информации при m числе выборке с вероятностью Рi каждой выборки определится выражением:

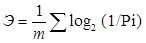
Алгоритмическая оценка информации характеризуется сложностью (размером) алгоритма (программы), которая позволяет ее произвести. На разных машинах и разных языках программирования такая оценка может быть разной. Поэтому задаются некоторой вычислительной машиной (например, элементарной машиной Тьюринга), а предлагаемая количественная оценка информации определяется сложностью слова, как минимальное число внутренних состояний машины, требуемой для его воспроизведения.

Структурная схема машины Тьюринга приведена на рисунке 2.2.

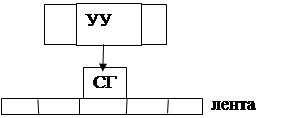
Рисунок 2.2 – Структурная схема машины Тьюринга

На рисунке 2.2 обозначено:

УУ – управляющее устройство;

СГ – считывающая головка;

Лента – источник информации бесконечная лента.

Управляющее устройство УУ определяет положение считывающей головки СГ {q_i}. В каждой ячейке ленты записан символ {a_i}. Таким образом, состояние машины {s_i} определится выражением:

S_i = q_i × a_i

Следующее перемещение ленты задается параметром {p_i}. Тогда новое состояние машины определится следующим образом:

S_i+1 = q_i × a_i ×p_i .

Таким образом, полное состояние машины Тьюринга можно задать, определив множества Q{qi}, A{ai}, P{pi}. Алгоритм определения состояния машины Тьюринга является единицей алгоритмического метода оценки информации.