Перевод чисел в системах счисления
При переводе чисел из одной системы счисления в десятичную систему счисления используют полином представления числа в Q-итой системе счисления, а затем выполняют арифметические операции в десятичной системе счисления, например:
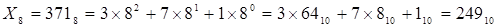
Например: перевод числа шестнадцатеричной системы af416 в десятичную систему счисления:
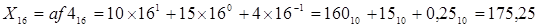
При обратном переводе чисел рассмотрим отдельно два случая перевода: целые и дробные числа.
4.1 Перевод целых чисел из Р-итой системы счисления в Q-ичную.
В соответствии с представлением целого числа в системе Р по основанию в системе Q имеем:
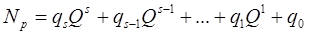 .
.
Разделим правую и левую часть на Q в результате получим новую целую часть и дробную часть (остаток):
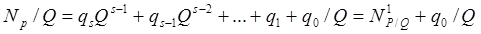 .
.
Проделав тоже самое, но уже с новым целым числом  , получим другой остаток
, получим другой остаток 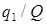 и другое целое число, с которым продолжим выполнение предыдущих операций, пока в остатке не получится число
и другое целое число, с которым продолжим выполнение предыдущих операций, пока в остатке не получится число 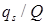 . Чтобы достичь этого, исходное число необходимо разделить на
. Чтобы достичь этого, исходное число необходимо разделить на
Q s+1 раз. При этом получаемый остаток будет описывать число в новой системе счисления Q, начиная с младшего разряда.
Пример: перевод число 9810 десятичной системы счислений в двоичную.

Остаток отображает число в двоичной системе счисления, начиная с младшего двоичного разряда:
Проверка осуществляется выполнением обратной операции:
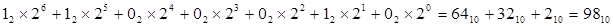
Дата добавления: 2021-03-18; просмотров: 546;











