Взаимная информация
Определим теперь информацию, содержащуюся в одном ансамбле относительно другого, например, в принятом сигнале относительно переданного сообщения. Для этого рассмотрим сообщение двух дискретных ансамблей A и B, вообще говоря, зависимых. Его можно интерпретировать как пару ансамблей сообщений, либо как ансамбли сообщения и сигнала, с помощью которого сообщение передаётся, либо как ансамбли сигналов на входе и выходе канала связи и т. д. Пусть P(ak ,bl)совместная вероятность реализаций ak и bl . Cовместной энтропией ансамблей A и B будем называть:
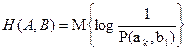 (2.6)
(2.6)
Введём также понятие условной энтропии:
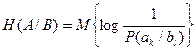 (2.7)
(2.7)
где P(ak / bl)- условная вероятность ak , если имеет место bl , здесь математические..
Из теоремы умножения вероятностей 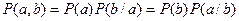 следует, что
следует, что 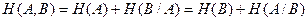 .
.
(2.8)
Для условной энтропии справедливо двойное неравенство:
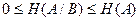 (2.9)
(2.9)
Рассмотрим два крайних случая:
1. Равенство 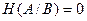 имеет место в том случае, когда, зная реализацию
имеет место в том случае, когда, зная реализацию 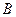 , можно точно установить реализацию
, можно точно установить реализацию 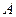 . Другими словами,
. Другими словами, 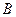 содержит полную информацию об
содержит полную информацию об 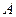 .
.
2. Другой крайний случай , когда 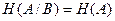 имеет место, если события
имеет место, если события 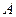 и
и 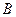 независимые. В этом случае знание реализации
независимые. В этом случае знание реализации 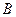 не уменьшает неопределённости
не уменьшает неопределённости 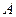 , т.е.
, т.е. 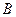 не содержит ни какой информации об А.
не содержит ни какой информации об А.
В общем случае, что имеет место на практике, условная энтропия 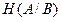 меньше безусловной
меньше безусловной 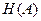 и знание реализации
и знание реализации 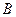 снимает в среднем первоначальную неопределённость
снимает в среднем первоначальную неопределённость 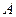 . Естественно, назвать разность
. Естественно, назвать разность 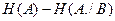 количеством информации, содержащейся в
количеством информации, содержащейся в 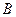 относительно
относительно 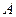 . Её называют также взаимной информацией между
. Её называют также взаимной информацией между 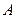 и
и 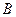 и обозначают
и обозначают 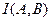 :
:
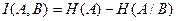 (2.10)
(2.10)
Подставляя в эту формулу значения H(A) и H(A/B) выразим взаимную информацию через распределение вероятностей:
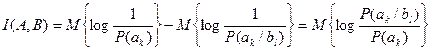 (2.11)
(2.11)
Если воспользоваться теоремой умножения 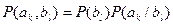 , то можно записать
, то можно записать 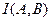 в симметричной форме т.к.
в симметричной форме т.к. 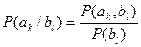 :
:
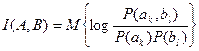 (2.12)
(2.12)
Взаимная информация измеряется в тех же единицах, что и энтропия. Величина 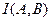 показывает, сколько мы в среднем получаем бит информации о реализации ансамбля
показывает, сколько мы в среднем получаем бит информации о реализации ансамбля 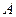 , наблюдая реализацию ансамбля
, наблюдая реализацию ансамбля 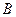 .
.
Сформулируем основные свойства взаимной информации:
1. 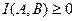 , причём равенство имеет место тогда и только тогда, когда
, причём равенство имеет место тогда и только тогда, когда 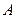 и
и 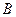 независимы между собой
независимы между собой
2. 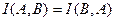 , то есть
, то есть 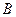 содержит столько же информации относительно
содержит столько же информации относительно 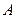 , сколько
, сколько 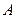 содержит относительно
содержит относительно 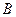 . Это свойство вытекает из симметрии выражения. Поэтому можно также записать:
. Это свойство вытекает из симметрии выражения. Поэтому можно также записать:
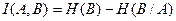 (2.13)
(2.13)
3. 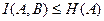 , причём равенство имеет место, когда по реализации
, причём равенство имеет место, когда по реализации 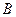 можно точно установить реализацию
можно точно установить реализацию 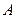 .
.
4. 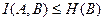 , причём равенство имеет место, когда по реализации
, причём равенство имеет место, когда по реализации 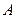 можно точно установить реализацию
можно точно установить реализацию 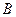 .
.
5. Полагая 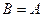 и учитывая, что
и учитывая, что 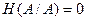 получим:
получим:
 (2.14)
(2.14)
Это позволяет интерпретировать энтропию источника как его собственную информацию, то есть информацию, содержащуюся в ансамбле 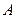 о самом себе.
о самом себе.
Пусть 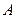 - ансамбль дискретных сообщений, а
- ансамбль дискретных сообщений, а 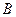 - ансамбль дискретных сигналов, в которые преобразуются сообщения
- ансамбль дискретных сигналов, в которые преобразуются сообщения 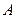 . Тогда
. Тогда 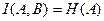 в том и только в том случае, когда преобразование
в том и только в том случае, когда преобразование 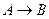 обратимо. При необратимом преобразовании
обратимо. При необратимом преобразовании 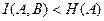 и разность
и разность 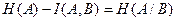 можно назвать потерей информации при преобразовании
можно назвать потерей информации при преобразовании 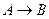 . Её называют ненадёжностью. Таким образом, информация не теряется только при обратимых преобразованиях.
. Её называют ненадёжностью. Таким образом, информация не теряется только при обратимых преобразованиях.
Если 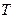 - среднее время передачи одного сообщения, то разделив на
- среднее время передачи одного сообщения, то разделив на 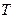 формулы H(A/B) и I(A,B) и обозначая:
формулы H(A/B) и I(A,B) и обозначая:
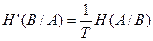 ,
, 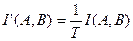 , (2.15)
, (2.15)
получим соответствующие равенства для энтропии и количества информации, рассчитанных не на одно сообщение, а на единицу времени. Величина 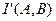 называется скоростью передачи информации от
называется скоростью передачи информации от 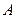 к
к 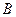 (или наоборот).
(или наоборот).
Рассмотрим пример: если 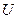 - ансамбль сигналов на входе дискретного канала, а
- ансамбль сигналов на входе дискретного канала, а 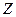 - ансамбль сигналов на его выходе, то скорость передачи информации по каналу.
- ансамбль сигналов на его выходе, то скорость передачи информации по каналу.
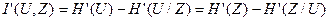 (2.16)
(2.16)
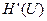 - производительность источника передаваемого сигнала
- производительность источника передаваемого сигнала 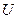 .
.
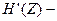 “производительность канала”, то есть полная собственная информация о принятом сигнале за единицу времени.
“производительность канала”, то есть полная собственная информация о принятом сигнале за единицу времени.
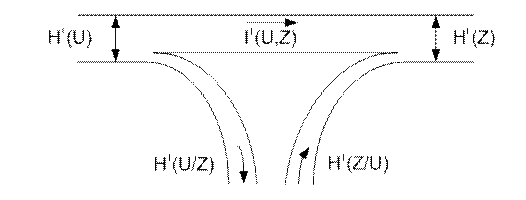
Величина 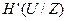 представляет собой скорость “утечки” информации при прохождении через канал, а
представляет собой скорость “утечки” информации при прохождении через канал, а 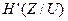 - скорость передачи посторонней информации, не имеющий отношения к
- скорость передачи посторонней информации, не имеющий отношения к 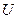 и создаваемой присутствующими в канале помехами. Соотношение между
и создаваемой присутствующими в канале помехами. Соотношение между 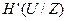 и
и 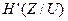 зависит от свойств канала. Так, например, при передаче телефонного сигнала по каналу с узкой полосой пропускания, недостаточной для удовлетворительного воспроизведения сигнала, и с низким уровнем помех теряется часть полезной информации, но почти не получается бесполезной. В этом случае
зависит от свойств канала. Так, например, при передаче телефонного сигнала по каналу с узкой полосой пропускания, недостаточной для удовлетворительного воспроизведения сигнала, и с низким уровнем помех теряется часть полезной информации, но почти не получается бесполезной. В этом случае 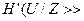
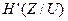 . Если же расширяется полоса, сигнал воспроизводится точно, но в паузах ясно прослушиваются “наводки” от соседнего телефонного канала, то, почти не теряя полезной информации, можно получить много дополнительной, как правило, бесполезной информации и
. Если же расширяется полоса, сигнал воспроизводится точно, но в паузах ясно прослушиваются “наводки” от соседнего телефонного канала, то, почти не теряя полезной информации, можно получить много дополнительной, как правило, бесполезной информации и 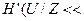
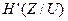 .
.
Дата добавления: 2016-07-22; просмотров: 2358;











