Взаимная информация и ее свойства

Определим теперь количество информации, передаваемой по каналу связи 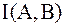как разность между количеством информации на его входе, равной энтропии источника 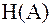и количеством потерянной информации, которая равна условной энтропии 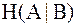. Величину 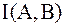называют также взаимной информацией и определяют соотношением:

;

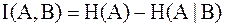(3.1)

или

;

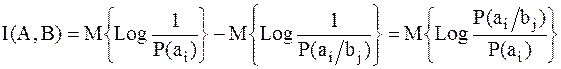(3.2)

С учетом теоремы умножения вероятностей получим:

;

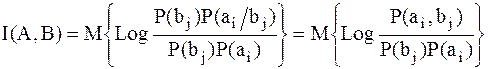(3.3)

Раскрывая последнее выражение, получим соотношение для взаимной информации в симметричном виде:

;

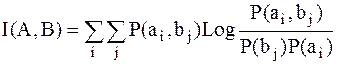(3.4)

Рассмотрим основные свойства взаимной информации:

1. 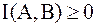. Это свойство следует из свойств энтропии, причём 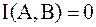при обрыве канала, когда вся информация теряется из-за помех в канале.

2. 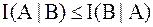. Равенство достигается при отсутствии помех, т. е. .

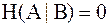3. 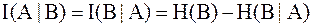, где энтропия выхода канала H(B) и условная энтропия 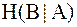определяются аналогично найденным выше значениям энтропии. Данное свойство вытекает из симметрии выражения для взаимной информации.

4. 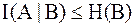. Данное свойство вытекает из предыдущего. Равенство здесь имеет место, если .

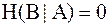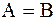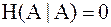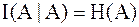5. В выражении для взаимной информации будем полагать , тогда , а . Таким образом, энтропию можно трактовать как меру собственной информации об ансамбле 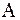источника сообщений.

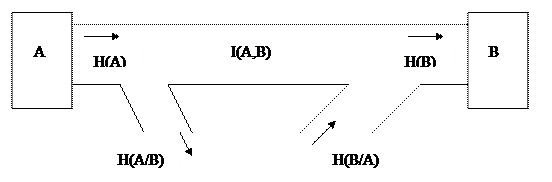
Определение взаимной информации наглядно иллюстрируется на рис. 2.

Рис. 2. Иллюстрация передачи информации по каналу с помехами

Пусть известно время передачи одного сообщения 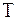, тогда по аналогии с производительностью источника можно легко определить скорость передачи информации по каналу как количество информации, переданной в единицу времени:

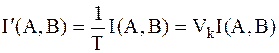;	(3.5)
где		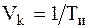–	скорость, т.е. число символов, поступающих в канал в течении секунды, бит/с (Бод).

Выводы

1. Взаимная информация представляет собой разность между количеством информации на входе канала связи, равной энтропии источника 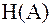и количеством потерянной информации, которая равна условной энтропии .

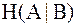Заключение

1. Из всех видов возможных распределений вероятностей случайных процессов, у которых дисперсия 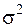является фиксированной величиной, наибольшее значение дифференциальной энтропии имеет гауссовское распределение.

2. Условная энтропия представляет собой количество информации, которое теряется из-за помех и не поступает получателю.

3. Взаимная информация представляет собой разность между количеством информации на входе канала связи, равной энтропии источника 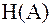и количеством потерянной информации, которая равна условной энтропии .

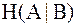Литература

1. Р.Р. Биккенин, М.Н. Чесноков Теория электрической связи. Случайные процессы. Помехоустойчивая передача дискретной информации: Учебное пособие / СПб., 2001, стр. 121-127.

2. Д.Д. Кловский «Теория электрической связи» М. «Радио и связь», стр. 246-249, 227-231.