Модели линз из призм. Ход лучей в линзах

1. Модель из двух призм. 1) Две трехгранные стеклянные призмы. 2) Источник света. 3) Ширма с двумя щелями.

На пути двух параллельных лучей света помещают по призме двумя способами. В первом случае призмы обращены друг к другу своими основаниями (рис. 340, I) и собирают падающие лучи, представляя принцип действия собирающей линзы. Во втором случае призмы обращены основаниями наружу и потому рассеивают лучи подобно рассеивающей линзе (рис. 340, II).

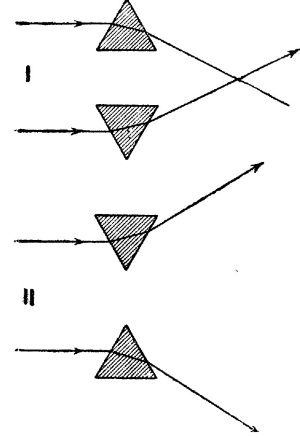
Рис. 340. Модель линз из призм

Прибор Гримзеля. 1) Четыре стеклянных сосуда для составления линз. 2) Источник света. 3) Приспособление Гримзеля для получения параллельных лучей (рис. 341).

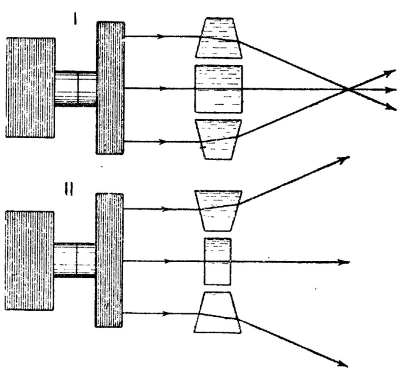
Рис. 341. Модель линз по Гремзелю

Четыре сосуда представляют собой две призмы (усеченные) и две плоско-параллельные пластинки разной толщины. Сосуды складывают вместе, помещая один на другой, причем в середине должна оказаться плоско-параллельная пластинка, а над и под нею — призмы. Если призмы приложены к (большой) плоско-параллельной пластинке своими широкими основаниями, получается модель собирающей линзы (рис. 341, I); если же призмы приложены к (меньшей) плоско-параллельной пластинке своими узкими основаниями, то прибор рассеивает лучи и изображает собой рассеивающую линзу (рис. 341, II).

Прибор „Станкин“. 1) Две ширмы с тремя стеклами каждая. 2) Источник света. Экспериментальная мастерская при физической лаборатории московского Станкоинструментального института („Станкин“) выпустила в продажу универсальную оптическую скамью (копию скамьи фирмы Spindler und Ноуег (т. І, рис. 240). Среди принадлежностей у скамьи имеются членистые выпуклая и вогнутая линзы, состоящие каждая из трех частей — плоско-параллельной пластинки и двух призм (рис. 342). Действие прибора такое же, как в опыте 2.

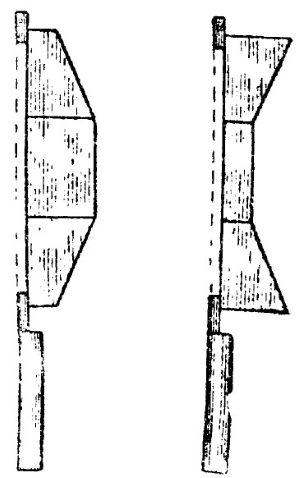
Рис. 342. Модель линз из набора «Станкин»

Ход лучей в линзах. Шайба Гартля. 1) прибор. 2) Двояковыпуклое стекло (№ 6 из набора). 3) Двояковогнутое стекло (№ 7 из набора). 4) Источник света. 5) Линеечка. 6) Карандаш для писания на стекле.

Стекло при помощи двух зажимных винтов (по концам) укрепляют на шайбе так, чтобы середина (оптический центр) стекла совпала с центром шайбы, оптическая ось стекла совпала с нулевым диаметром. Установку проверяют, направив на стекло падающий луч вдоль нулевого диаметра; тогда выходящий луч должен идти тоже вдоль этого диаметра (рис. 343, I).

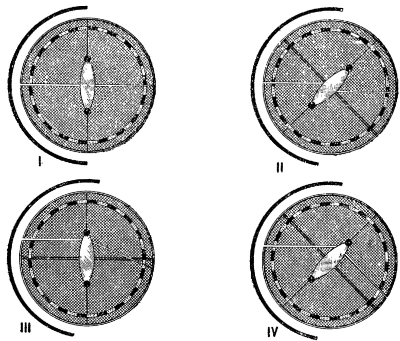
Рис. 343. Шайба Гартля (ход лучей в двояковыпуклой линзе)

Когда установка готова, направляют на стекло один луч (открыта одна средняя щель) и, меняя его расположение относительно стекла поворотом шайбы и ширмы, показывают учащимся следующие случаи хода лучей в двояковыпуклой линзе.

Случай 1. Луч, проходящий через оптический центр линзы, идет, не изменяя своего направления (луч испытывает сдвиг тем меньший, чем тоньше линза).

Поворачивают шайбу так, чтобы луч внутри стекла проходил всегда через его середину. Для этого придется чуть сдвинуть шайбу (щель), (рис. 343, II). Опыт повторяют несколько раз, направляя луч под разными углами.

Случай 2. Луч, идущий параллельно главной оптической оси стекла, по выходе из стекла проходит через фокус стекла.

Восстановив основную установку, не трогают шайбу и сдвигают ширму (щель) так, чтобы луч шел параллельно оптической оси стекла, т. е. (соответственно начальной установке) параллельно нулевому диаметру (рис. 343, III). Если падает пучок непараллельных лучей (немного расходящихся), то, кроме того, придется немного повернуть шайбу. Точка нулевого диаметра, через которую пройдет луч после стекла, будет фокусом стекла (назовем его первым, F₁). Этот фокус отмечают карандашом (для писания на стекле) и, повторяя опыт с несколькими падающими лучами, обнаруживают, что все такие лучи после стекла проходят через фокус.

Вернувшись к основной установке, поворачивают шайбу на 180° (так что лучи будут падать с другой стороны стекла, чем в предыдущем опыте), повторяют опыт и находят второй фокус стекла (обозначим его через F₂). Положение его отмечают на шайбе. Обращают внимание учащихся на одинаковое расстояние от стекла обоих фокусов (примерно 8—9 см).

Случается, что с одного раза положение фокуса определяется не совсем верно. Это скажется при повторных опытах, поэтому полезно заранее отыскать фокусы и, проверив их положение, отметить их карандашом (обычным) на шайбе.

Случай 3. Луч, проходящий через фокус линзы, после нее идет параллельно главной оптической оси.

Поворотом шайбы и ширмы направляют луч через фокус F₁. Тогда после стекла луч должен пойти параллельно главной оптической оси, т. е. нулевому диаметру (рис. 343, IV). Эту установку удобнее выполнять по выходящему лучу, чем по падающему, т. е. надо устанавливать шайбу так, чтобы выходящий из стекла луч был параллелен нулевому диаметру. Тогда падающий луч должен пройти через фокус. Опыт повторяют с несколькими лучами и с обоими фокусами.

Если вместо узкого (b = З см) двояковыпуклого стекла взять более широкое (b = 4,5 см) стекло (№ 8 из набора), имеющее меньшие радиусы или большую кривизну, то можно показать, как величина фокусного расстояния зависит от кривизны. У более толстого стекла фокусное расстояние примерно 6—7 см, т. е. оно уменьшается с увеличением кривизны.

Двояковыпуклое стекло заменяют двояковогнутым (№ 7 из набора) и устанавливают его совершенно так же (рис. 344, I), как устанавливали двояковыпуклое. Затем производят аналогичную серию опытов, разбив их на три случая.

Случай 1. Луч, проходящий через оптический центр линзы, не меняет своего направления, но испытывает сдвиг.

Надо заметить, что сдвиг у двояковогнутого стекла будет меньше, чем у выпуклого, поскольку вогнутое стекло в своей середине тоньше выпуклого (рис. 344, II). Опыт производится таким же образом, как и с двояковыпуклым стеклом.

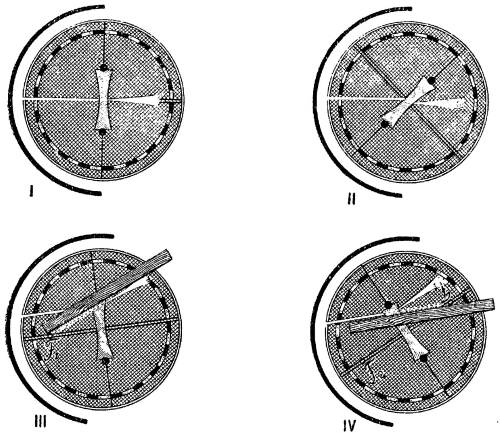
Рис. 344. Шайба Гартля (ход лучей в двояковогнутой линзе)

Случай 2. Луч, идущий параллельно главной оптической оси, после стекла идет так, что продолжение луча проходит через фокус (лежащий перед стеклом).

Установку производят так же, как и для двояковыпуклого стекла, но дальше придется поступить иначе: чтобы найти фокус, надо приложить к прошедшему через стекло лучу линеечку и найти точку ее пересечения с нулевым диаметром (оптической осью) перед стеклом (рис. 344, III). Эта точка и будет первым (мнимым) фокусом линзы. На шайбе отмечают положение первого фокуса (F₁) карандашом (для писания на стекле).

Как это было сказано относительно двояковыпуклого стекла, и в данном случае целесообразно отыскать положение фокуса заранее и наметить его на шайбе. Повернув шайбу на 180°, направляют луч света на стекло с другой его стороны и, повторив тот же опыт, находят второй (мнимый) фокус (F₂) линзы; показывают учащимся, что оба фокуса лежат на одинаковых расстояниях от стекла.

Так как двояковогнутое стекло рассеивает свет, то лучи, прошедшие через стекло, дают на экране светлые полоски, постепенно расширяющиеся и потому быстро теряющие свою яркость. Такие лучи трудно проследить на экране на большом расстоянии и часто с трудом удается дотянуть их до градусных делений. Большая ширина полоски затрудняет решение вопроса о фиксировании направления луча; приходится за его направление принимать среднюю линию полоски.

Случай 3. Луч, идущий так, что его продолжение (по другую сторону стекла) проходит через фокус линзы, после линзы идет параллельно главной оптической оси.

Как и в случае выпуклого стекла, установку удобнее производить по вышедшему из стекла лучу, т. е. поворотами шайбы и ширмы со щелью добиться, чтобы луч после стекла шел параллельно нулевому диаметру. Тогда продолжение падающего луча по другую сторону стекла должно пройти через фокус линзы; в этом убеждаются, прикладывая линеечку к падающему лучу (рис. 344, IV). Опыт повторяют с несколькими падающими лучами и с обоими фокусами.

Надо обратить внимание учащихся на взаимную обратимость второго и третьего случаев хода лучей в линзах. Об этой обратимости было сказано раньше (§ ЗО, 1); знание этой обратимости облегчает запоминание всех случаев хода лучей.