Свободные гармонические колебания в колебательном контуре

Среди различных электрических явлений особое место занимают электромагнитные колебания, при которых электрические величины (заряды, токи) периодически изменяются и которые сопровождаются взаимными превращениями электрического и магнитного полей. Для возбуждения и поддержания электромагнитных колебаний используется колебательный контур.

На схеме (рис. 16.1) условно изображен идеальный колебательный контур, состоящий из емкости 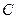и индуктивности 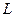, но не обладающий сопротивлением.

Рассмотрим процессы, происходящие при незатухающих колебаниях в колебательном контуре.

Разность потенциалов 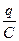между обкладками конденсатора ( 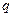– заряд одной из обкладок) равна ЭДС индукции 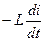, возникающей в катушке ( 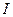– сила тока в катушке). Итак,

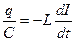
Но

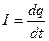
и, следовательно,

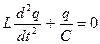
введя обозначение собственной частоты контура 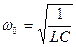, получим

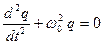, (16.1.1)

Уравнение (16.1.1) является дифференциальным уравнением свободных гармонических колебаний в колебательном контуре. Если конденсатор имеет начальный заряд или если в катушке возбужден начальный ток (например, в результате движения магнита около катушки), в контуре происходят электрические гармонические колебания

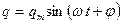
где 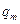- амплитуда колебаний заряда конденсатора.

Период колебаний в колебательном контуре

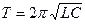
Формула впервые была получена У. Томсоном и называется формулой Томсона.

Сила тока и напряжение в колебательном контуре меняется по закону

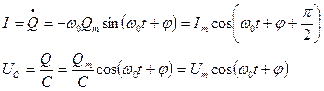
где 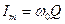- амплитуда силы тока, 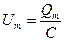- амплитуда напряжения. Из уравнений следует, что колебания тока опережает по фазе колебания заряда, т.е. когда ток достигает максимального значения, заряд (а также и напряжение) обращается в нуль, и наоборот.