Давление под искривленной поверхностью жидкости.

Если поверхность жидкости не плоская, то стремление ее к сокращению приведет к возникновению давления, дополнительного к тому, которое испытывает жидкость с плоской поверхностью. В случае выпуклой поверхности это дополнительное давление положительно, в случае вогнутой поверхности - отрицательно.

Вычислим добавочное давление Dр для сферической поверхности жидкости (рис.9.13). Рассечем мысленно сферическую каплю жидкости диаметральной плоскостью на два полушария.

Из-за поверхностного натяжения оба полушария притягиваются с силой, равной

.

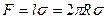Эта сила прижимает друг к другу оба полушария по поверхности 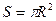и, следовательно, обусловливает дополнительное давление

.

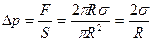Кривизна сферической поверхности всюду одинакова и определяется радиусом сферы R. Чем меньше R, тем больше кривизна поверхности. Для сферической поверхности кривизна Н=1/R.

Если форма поверхности несферическая, то Dр выражается через среднюю кривизну нормального сечения. Нормальным сечением поверхности называется линия пересечения поверхности плоскостью, проходящей через нормаль в данной точке. В геометрии доказывается, что полусумма обратных радиусов кривизны:

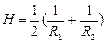(9.8.1)

для любой пары взаимно перпендикулярных нормальных сечений имеет одно и то же значение. Эта величина и есть средняя кривизна поверхности в данной точке.

Радиусы R₁ и R₂ в формуле (9.8.1) – алгебраические величины. Если центр кривизны нормального сечения находится под данной поверхностью, соответствующий радиус кривизны положителен; если центр кривизны лежит над поверхностью, радиус кривизны отрицателен. Неплоская поверхность может иметь среднюю кривизну, равную нулю. Для этого нужно, чтобы радиусы кривизны R₁ и R₂ были одинаковы по величине и противоположны по знаку.

Для сферы Н=1/R, поэтому

.

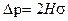Лаплас доказал, что эта формула справедлива для поверхности любой формы, если под Н понимать среднюю кривизну поверхности в той точке, под которой определяется дополнительное давление. Подставив сюда выражение для средней кривизны, получим формулу для добавочного давления под произвольной поверхностью:

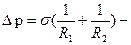формула Лапласа.

Для сферической искривленной поверхности (R₁=R₂=R) это выражение переходит в 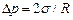, для цилиндрической (R₁=R, R₂=¥) – избыточное давление 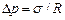. В случае плоской поверхности (R₁=R₂=¥) силы поверхностного натяжения избыточного давления не создают. Добавочное давление обуславливает изменение уровня жидкости в узких трубках (капилляр), вследствие чего оно еще называется капиллярным давлением.

Капиллярность.

Изменение высоты уровня жидкости в узких трубках или зазорах получило название капиллярности. (Лат. capillus) означает волос. Капилляр – «трубка, тонкая, как волос»).

Если опустить капилляр в смачиваемую жидкость, то под действием лапласовского давления жидкость в нем поднимается (рис.9.14). Между жидкостью в капилляре и широком сосуде устанавливается разность уровней h, при которой капиллярное (добавочное) давление уравновешивается гидростатическим:

.

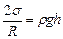где R – радиус мениска. Выразим радиус мениска через краевой угол q и радиус капилляра r: 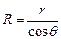. Тогда высота поднятия жидкости в капилляре:

.

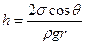Смачивающая жидкость (q<p/2, cos q>0) поднимается по капилляру(рис.9.14 - вода), и эта формула дает положительное значение h, а несмачивающая жидкость (q>p/2, cos q<0) опускается по капилляру(рис.9.14 - ртуть), и формула дает отрицательные значения h. Из полученного выражения видно, что высота поднятия (опускания) жидкости в капилляре обратно пропорциональна его радиусу. В тонких капиллярах жидкость поднимается достаточно высоко.

Рассмотрим поднятие смачивающей жидкости между двумя пластинами, разделенными узким зазором d. Если пластины параллельны, то мениск имеет цилиндрическую форму. Высота капиллярного подъема в этом случае также определяется из условия равенства лапласовского Δр и гидростатического давлений. Для цилиндрической поверхности R₁=R - радиус цилиндра, R₂=Ґ, поэтому избыточное давление за счет искривления поверхности: 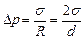, тогда высота капиллярного подъема в этом случае:

.

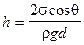Капиллярные явления имеют большое значение в природе и технике. Например, влагообмен в почве и в растениях осуществляется за счет поднятия воды по тончайшим капиллярам. В капилляре переменного сечения капля смачиваемой жидкости под воздействием разности лапласовских давлений втягивается в сторону его утончения. Этим объясняется так называемое расклинивающее действие смачивающих жидкостей: жидкости, проникая в микротрещины, увеличивают их и тем самым понижают прочность твердых тел. На капиллярности основано действие фитилей, впитывание влаги бетоном и т.д.