Кинематика материальной точки и поступательного движения твердого тела

Система отсчета. Траектория.

Длина пути и вектор перемещения

Для описания движения тела в пространстве и времени используют физические модели:

· Материальной точкой (тело точечной массы) называется идеализированная модель, соответствующая физическому телу, размерами которого в данных условиях можно пренебречь.

· Абсолютно твердое тело – тело, расстояние между двумя точками которого в условиях данной задачи можно считать постоянным. Иначе говоря - это тело, формы и размеры которого не изменяются при его движении.

· Абсолютно упругое тело – тело, деформация которого подчиняется закону Гука, а после прекращения внешнего силового воздействия восстанавливает свои первоначальные размеры и форму

· Абсолютно неупругое тело – тело, сохраняющее деформированное состояние после прекращения действия внешних сил.

Всякое тело можно мысленно разбить на большое число частей, сколь угодно малых по сравнению с размерами всего тела. Каждую такую часть можно рассматривать как материальную точку, а само тело или любую систему тел – как систему материальных точек.

Положение тел в пространстве можно определить только по отношению к другим телам. Абсолютно твердое тело, по отношению к которому рассматривают движение исследуемого тела, называется системой отсчета. С системой отсчета жестко связывают систему координат, так что положение любой точки определятся значениями трех координат этой точки. Наиболее часто пользуются прямоугольными декартовыми координатами: x, y, z (рис.1.1.).

Положение точки М относительно системы отсчета можно задать не только с помощью трех ее декартовых координат x, y, z, но также с помощью векторной величины - проведенного в точку М из начала системы координат (точки О) радиуса - вектора 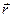(рис. 1.1). Если - единичные вектора осей прямоугольной декартовой системы координат, то

(1.1.1)

При движении материальной точки М ее координаты x, y, z и 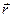меняются со временем. Поэтому для определения положения материальной точки в любой момент времени (t) вводятся уравнения, которые в декартовой системе координат имеют вид:

,

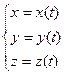(1.1.2,а)

или в более общей записи

.

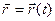(1.1.2,б)

Зависимости (1.1.2,а) и (1.1.2,б) называются кинематическими уравнениями движения материальной точки.

Совокупность всех последовательных положений материальной точки в пространстве представляет траекторию движения. В зависимости от формы траектории различают прямолинейное и криволинейное движение точки. Движение точки называется плоским, если ее траектория целиком лежит в одной плоскости.

Длиной пути S материальной точки называют сумму длин всех участков траектории, пройденных этой точкой за рассматриваемый промежуток времени.

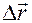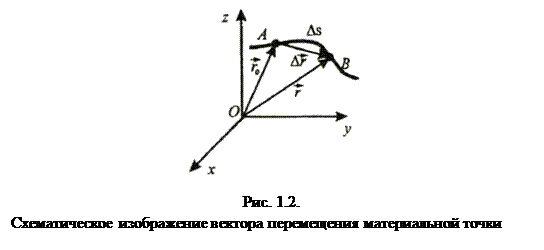
Вектором перемещения материальной точки за время 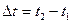называется вектор, проведенный из положения этой точки в момент времени t₁ в ее положение в момент t₂ (рис. 1.2.). Он равен приращению радиус-вектора 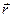за рассматриваемый промежуток времени Dt:

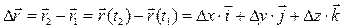
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории.

Для измерения длины пути и перемещения используют меру длины – метр (м) в системе СИ и – сантиметр (см) в системе СГС.

Материальная точка, свободно движущаяся в пространстве, может совершать только три независимых движения. Например, движение точки вдоль каждой из осей прямоугольной декартовой системы координат нельзя осуществить за счет ее движения вдоль остальных двух осей. Число независимых движений, которые может совершать механическая система, называется числом степеней свободы этой системы. Следовательно, свободная материальная точка имеет три степени свободы.

Скорость

Для характеристики быстроты движения материальной точки вводят векторную физическую величину – скорость.

Пусть в момент t₁ материальная точка, движущая по некоторой траектории, находилась в положении А (x₁, y₁, z₁), характеризуемом радиус– вектором 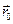, в момент времени t₂ – в положении В (x₂, y₂, z₂), характеризуемом радиус – вектором 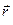(рис. 1.2). Таким образом, за интервал времени Dt= t₂- t₁ материальная точка прошла криволинейный отрезок АВ=DS.

Вектором средней скорости 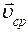точки в интервале от t₁ до t₂ называется

(1.1.3)

Из формулы (1.1.3) видно, что вектор средней скорости 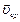совпадает по направлению с вектором перемещения 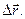При неограниченном уменьшении времени, т.е. Dt ® 0, то средняя скорость стремиться к предельному значению, которое называется мгновенной скоростью

.

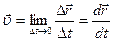(1.1.4)

Вектор мгновенной скорости направлен по касательной к данной точки траектории. Из математики известно, что при DS ® 0 DS/Dr = 1 и, как следствие, В этом случае можно ввести понятие путевой скорости:

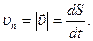(1.1.5)

Из уравнения (1.1.5) можно определить путь, пройденный точкой за данный промежуток времени: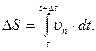

Поскольку мгновенная скорость 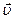- векторная величина, то ее можно разложить на три составляющие по осям координат, то есть

(1.1.6)

Используя выражения (1.1.1) и (1.1.4), можно показать, что

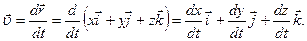
(1.1.7)

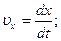
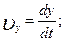
Сравнивая выражения (1.1.6) и (1.1.7), можно определить проекции вектора скорости на декартовые оси координат: 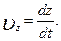Последние позволяют рассчитать модуль скорости в данный момент времени:

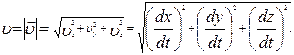
В системе СИ единицей измерения скорости является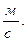

Ускорение

Величиной, характеризующей быстроту изменения скорости, является ускорение.

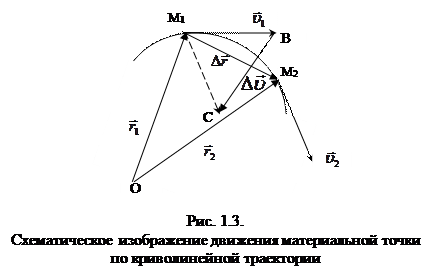На рисунке 1.3. показан участок траектории движения материальной точки. Пусть в момент времени t₁ материальная точка находилась в положении М₁ и двигалась со скоростью 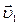, в момент времени t₁ – в М₂ и имела скорость 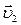. Изменение скорости за интервал времени Dt: 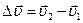(на рис. 1.3. соответствует вектору ).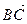

Средним ускорением неравномерного движения в интервале Dt называется векторная величина, равная отношению изменения скорости к интервалу времени

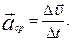
(1.1.8)

Как видно из формулы, вектор среднего ускорения сонаправлен с вектором изменения скорости .

Ускорением или мгновенным ускорением точки в момент времени t называется величина

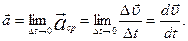
(1.1.9)

Так как мгновенное ускорение – векторная величина, то

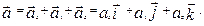
(1.1.10)

Из выражений (1.1.6) и (1.1.9) следует и, как следствие:

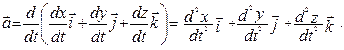
(1.1.11)

Таким образом, из (1.1.10) и (1.1.11) следует, что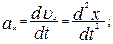

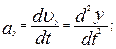
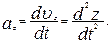
Модуль вектора ускорения равен

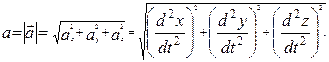
При рассмотрении плоского движения удобно пользоваться скользящей системой координат – системой, которая изменяет свое положение в пространстве вместе с движением материальной точки, то есть за начало отсчета принимают саму движущуюся точку. Одна ось вышеуказанной системы направлена по касательной к траектории движения материальной точки в данный момент времени (тангенциальная или касательная ось ), другая направлена перпендикулярно первой, и называется нормальной осью 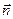(см. рис. 1.4).

Рассмотрим движение точки вдоль криволинейной траектории MN (см. рис.1.4). В скользящей системе координат скорость материальной точки можно представить как 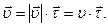Из выражения (1.1.9) следует, что

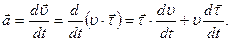
Таким образом, ускорение материальной точки представляет собой сумму двух векторов:

1) тангенциальное ускорение, которое показывает быстроту изменение модуля скорости материальной точки:

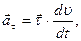
2) нормальное ускорение показывает быстроту изменения направления скорости:

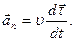
Величина полного ускорения

(1.1.12)

Нормальное ускорение перпендикулярно тангенциальной оси и направлено по нормальной оси скользящей системы координат.

Для определения физического смысла нормального ускорения рассмотрим равномерное движение материальной точки по окружности (см. рис. 1.5). В момент времени t₁ материальная точка находилась в положении М₁ и двигалась со скоростью – 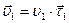, в момент t₂ – в положении М₂ и имела скорость 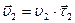. При равномерном движении модуль скорости остается постоянным (следовательно, тангенциальное ускорение равно нулю: 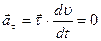), а направление вектора скорости меняется. Изменение единичного вектора равно . За малый промежуток времени dt модуль вектора dt можно определить как dt = t×dj, где dj - угол поворота вектора скорости материальной точки. Так как t = 1, то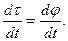

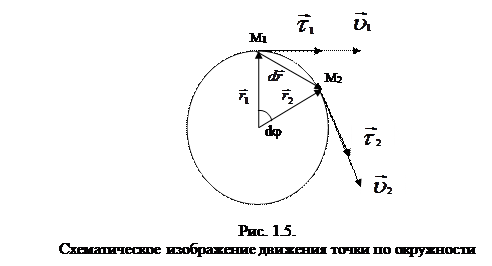Из рис. 1.5 видно, что dr =R×dj (R – радиус окружности).

Поэтому 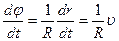. Из приведенных выше выводов следует, что

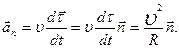
(1.1.13)

При прямолинейном движении нормальная составляющая полного ускорения равна нулю (так как 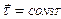и 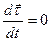). При равномерном движении по окружности, как отмечалось выше, 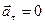. В общем случае при криволинейном движении имеют место и тангенциальная и нормальная составляющие полного ускорения, так что можно определить модуль полного ускорения: 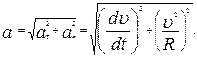Единицей измерения ускорения в системе СИ является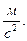

Рассмотрим несколько частных случаев:

1. Прямолинейное равномерное движение:

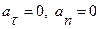, , причем 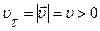. Поэтому

(1.1.14,а)

где x₀ – значение x в начальный момент времени (t = 0). Таким образом, для величины пути

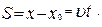
(1.1.14,б)

2. Прямолинейное равнопеременное движение:

a_n = 0, a_t = const. При a_t > 0 – движение равноускоренное; при a_t < 0 – движение равнозамедленное.

Из выражения (1.1.9) следует, что

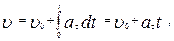
(1.1.15)

где 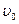– начальная скорость. Для координаты

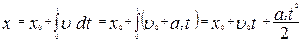
(1.1.16,а)

и пути

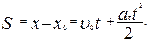
(1.1.16,б)

Часто для простоты записи в выражениях (1.1.15), (1.1.16,а) и (1.1.16,б) вместо a_t используют a.

3. Равномерное движение по окружности:

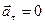, a_n = const. Так как численное значение скорости в этом виде движения является постоянной величиной, то величина скорости может быть определена через 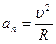. При R=const траектория движения является окружность. В этом случае ускорение a_n называют центростремительным.

4) a_n = const, a_τ = const – траекторией движения является спираль.