Пример расчета попадания точки в заданную область.
Задана таблица работоспособности объекта.
Работоспособность объекта Таблица 2.1.
| № п/п | x1 | x2 | работоспособность объекта |
| да | |||
| да | |||
| да | |||
| да | |||
| да | |||
| да | |||
| да |
Вопрос: будет ли работоспособен объект с параметрами 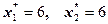 ?
?
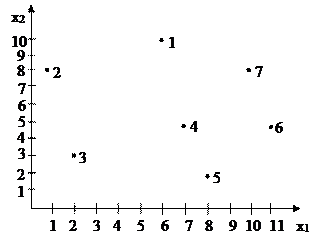 Решение. Геометрическое представление исходных данных отображено на рис. 2.4.
Решение. Геометрическое представление исходных данных отображено на рис. 2.4.
|
Рис. 2.4. Координаты исходных точек.
Из графического представления видно, что точка с координатами (6,6) попадает внутрь выпуклой области. Докажем этот факт аналитически, предварительно построив выпуклую область работоспособности заданного объекта.
Проведем построение области согласно алгоритму, изложенному в разделе 2.1.
1 шаг.Берется (N + 1) точки в N – мерном пространстве в нашем случае N=2, т.е.берем точки 1, 2, 3.
Через каждые N точек проводится гиперплоскость и заполняется таблица
| Прямая | 1 – 2 | 2 – 3 | 1 – 3 |
| Вершина | |||
| координаты вершин | 2; 3 | 6; 10 | 1; 8 |
| координаты 1-ой точки | 6; 10 | 1; 8 | 6; 10 |
| координаты 2-ой точки | 1; 8 | 2; 3 | 2; 3 |
| уравнение прямой | x1 – 2,5x2 + 19 = 0 | x1 + 0,2x2 – 2,6 = 0 | 7x1 - 4x2 – 2 = 0 |
2 шаг. Для точки 4 ищем генеральную гиперплоскость среди всех ранее построенных плоскостей. Является ли (1 – 2) генеральной гиперплоскостью для точки 4.
S (т.4) = 7 – 2,5 × 5 + 19 > 0
S¢ (т.3) = 2 – 2,5 × 3 + 19 > 0, т.е. (1-2), не является для точки 4 генеральной гиперплоскостью.
Для т. 4 генеральная гиперплоскость (1-3);
S¢ (т.4) = 7 × 7 – 4,5 - 2 > 0
S¢ (т.2) = 7 × 1 – 4,8 - 2 < 0, т.е. (1-3), является для точки 4 генеральной гиперплоскостью.
Мы снова имеем (N + 1) точку – это {1, 3, 4}
Через каждые N точек проведем гиперплоскости (в данном случае прямые)
Для упрощения построения часть таблицы не заполняется.
| Прямая | 1 – 3 | 3 – 4 | 1 – 4 |
| Вершина |
После обработки каждой точки генеральная гиперплоскость и плоскости повторяющиеся (одни и те же плоскости в разных таблицах) вычеркиваются.
3 шаг.Для точки 5 генеральная гиперплоскость (1 – 4)
| Прямая | 1 – 4 | 4 – 5 | 1 – 5 |
| Вершина |
а также (3 – 4)
| Прямая | 3 – 4 | 3 – 5 | 5 – 4 |
| Вершина |
4 шаг.Для точки 6 генеральная гиперплоскость (1 – 5)
| Прямая | 1 – 5 | 5 – 6 | 1 – 6 |
| Вершина |
5 шаг.Для точки 7 генеральная гиперплоскость (1 – 6)
| Прямая | 1 – 6 | 6 – 7 | 7 – 1 |
| Вершина |
Получили границу области работоспособности:
(1 – 2) – (2 – 3) – (3 – 5) – (5 – 6) – (6 – 7) – (7 – 1).
Окончательный шаг объекта для перехода от уравнений к неравенствам необходимо в линейную форму (левая часть равенства) поставить координаты вершины.
Если величина линейной формы положительна, то знак “=” заменяется на “³”, если же отрицательна то знак “=” заменяется на “£”.
Пример: (1 – 2): x1 – 2,5x2 + 19 = 0.
S¢(т.3) = 2 – 2,5 × 3 + 19 > 0.
Соответствующее неравенство имеет вид: x1 – 2,5x2 + 19 ³ 0.
Полученная область представлена на рис. 2.5.
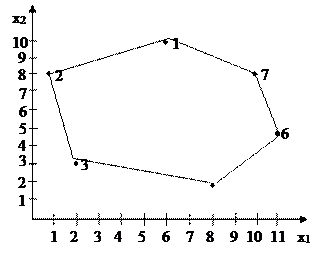 |
Рис. 2.5. Область решений системы неравенств.
Аналогично получаем всю совокупность неравенств, которые описывают область работоспособности объекта.
(1 – 2) Þ x1 – 2,5x2 + 19 ³ 0
(2 – 3) Þ x1 + 0,2x2 – 2,6 ³ 0
(3 – 5) Þ x1 + 6x2 - 20 ³ 0
(5 – 6) Þ -x1 + 0,75x2 + 6,5 ³ 0
(6 – 7) Þ -x1 – 0,5x2 +14 ³ 0
(7 – 1) Þ -x1 - 2x2 + 26 ³ 0
Проверка работоспособности объекта состоит в выполнении данных неравенств. Если хотя бы одно из неравенств не удовлетворяло условию, то точка не попадает в область. Данная методика позволяет исключить сбойные результаты в экспериментах на основе адаптивных (последовательных) процедур. Данный метод с удалением выпуклых оболочек (выпуклых слоев) предложил Тьюки. Процедура получила название «шелушение». Она позволяет при большом количестве точек измерения эффективно удалять сбойные результаты для объектов высокой размерности и, таким образом вести адаптивную обработку данных в задаче принятия решения о работоспособности объекта. Адаптивность в данном случае означает отбрасывание случайных результатов до тех пор, пока численные характеристики распределения случайной величины, например, вероятность, не будут постоянны. В рассмотренном примере сбойным результатом являлась точка 4. Построение линейной гиперплоскости для большого числа переменных не представляет сложной задачи и легко решается методами линейной алгебры.
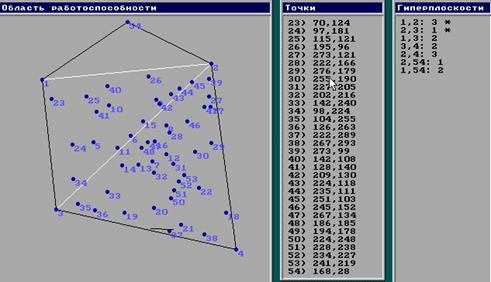
Рис. 2.6. Исключение сбойных результатов методом Тьюки.
Для проверки попадания точки с координатами (6; 6) в построенную область используем программу MS Excel. Все необходимые данные занести в таблицу, как показано на рис. 2.7.
В ячейках В4 и С4 записаны координаты заданной точки.
В ячейке D8 записана формула подстановки точки (6;6) в первое неравенство 6*1+6*(-2,5) = -9. В обозначениях Excel формула выглядит следующим образом: = СУММПРОИЗВ($B$4:$C$4;B8:C8).
В ячейку G8 занесена формула =D8>=F8, вычисляющая логическую функцию ИСТИНА или ЛОЖЬ. Окончательный результат записывается в ячейке G15 в виде = И(G8:G13). Это означает попадание заданной точки в построенную область.
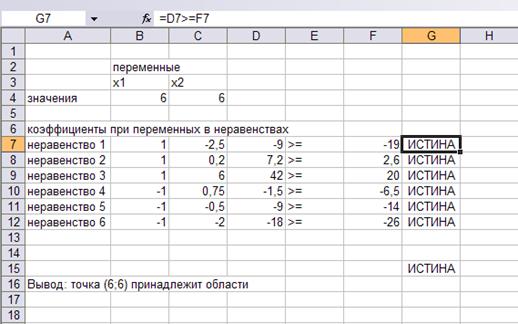
Рис. 2.7. Проверка попадания точки в заданную область.
Дата добавления: 2016-12-09; просмотров: 4534;











