Теоретико-множественный подход к определению вероятности события (геометрическая вероятность, аксиоматический подход).
Подход к нахождению вероятности, реализуемый в формуле (1.1)непосредственного подсчета вероятности можно использовать и тогда, когда множество равновозможных событий несчетно и интерпретируется как множество всех точек определенной области размера Sn, а множество событий, благоприятствующих событию А, интерпретируется определенной подобластью размера Sm; тогда
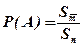 (1.2)
(1.2)
Поскольку данная формула предусматривает определение геометрических размеров (длин, площадей, объемов) областей, то вычислительную на ее основе вероятность часто называет еще геометрической.
Для решения задач с помощью данного подхода необходимо:
- уяснить существо и при необходимости дать словесную формулировку случайного события А, вероятность которого требуется нейти;
- построить область, точки которой интерпретируют все равновозможные события из определенной полной группы и найти ее размер – Sn;
- построить подобласть, все точки которой интерпретируют равновозможные события из определенной полной группы и благоприятствуют событию А; найти ее размер Sm;
- вычислитьотношение 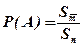 .
.
В условиях ряда задач на эту тему могут отсутствовать явные указания на равновозможность событий, тогда следует принять обоснованные допущения.
Пример 1.4. На отрезке единичной длины наугад и независимо друг от друга выбираются две точки. Какова вероятность, что расстояние между этими точками будет не менее 1/3?
Решение. Обозначим: А - событие, заключающееся в том, что расстояние между выбранными точками не менее 1/3.
Термин “наугад”, фигурирующий в условии, означает, что положение каждой точки равновозможно на отрезке единичной длины. Так как исход опыта характеризуется расположением двух точек, то естественно множество всех возможных исходов (событий), образующих полную группу, интерпретировать как множество точек "единичного" квадрата в системе t1 ° t2 (рис.1.1). Равновозможность выбора 1-ой точки на отрезке [0,l] оси оt1 и равновозможность выбора 2-ой точки на отрезке [0,1] оси оt2 обеспечивают равновозможность всех исходов опыта, интерпретируемых точками единичного квадрата.
 Размер (площадь) области всех равновозможных событие Sn = 1 × 1 = 1. Равновозможные события, благоприятствующие А, интерпретируются точками квадрата, для которых удовлетворяется условие
Размер (площадь) области всех равновозможных событие Sn = 1 × 1 = 1. Равновозможные события, благоприятствующие А, интерпретируются точками квадрата, для которых удовлетворяется условие 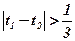 , т.е. отстоящими от диагонали по каждой из осей более чем на 1/3 (заштриховано на рис. 1.1). Площадь области благоприятных событий
, т.е. отстоящими от диагонали по каждой из осей более чем на 1/3 (заштриховано на рис. 1.1). Площадь области благоприятных событий
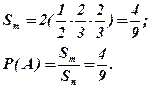
При теоретико-множественном подходе к определению вероятностей событий следует для упрощения вычислений использовать свойства теории множеств. Приведем некоторые из них, наиболее распространенные при такого рода вычислениях. Обозначим: W - множество всех исходов опыта; А, В - подмножества W, Æ - пустое множество.
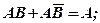 (1.3)
(1.3)
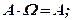 (1.4)
(1.4)
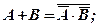 (1.5)
(1.5)
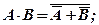 (1.6)
(1.6)
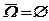 (1.7)
(1.7)
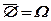 (1.8)
(1.8)
Аксиомы теории вероятностей на основе теоретико-множественного подхода впервые были введены А.Н. Колмогоровым. Событию А ставится в соответствие некоторое число, называемое вероятностью события.
Аксиома 1. Вероятность любого события заключена между нулем и единицей
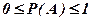 .
.
Аксиома 2. Если А и В несовместимые события (А × В = Æ), то
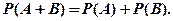 (1.9)
(1.9)
Аксиома 3. Вероятность достоверного события равна 1.
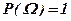 .
.
Аксиома 4. Сумма вероятностей противоположных событий равна единице
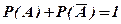 (1.10)
(1.10)
Пример 1.5. События А, В могут быть совместимыми (рис. 1.2). Какова вероятность Р(А + В)?
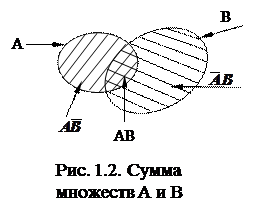 Решение. Непосредственно аксиомой 2 воспользоваться нельзя, т.к. она справедлива лишь для несовместимых событий. Чтобы использовать аксиомы, представим интересующее нас множество в виде суммы несовместимых событий.
Решение. Непосредственно аксиомой 2 воспользоваться нельзя, т.к. она справедлива лишь для несовместимых событий. Чтобы использовать аксиомы, представим интересующее нас множество в виде суммы несовместимых событий.
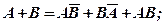 (1.11)
(1.11)
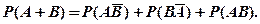 (1.12)
(1.12)

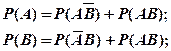
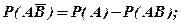 (1.13)
(1.13)
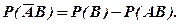 (1.14)
(1.14)
Подставляя выражения (I.I3), (I.I4) в (1.12), получаем
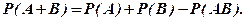 (1.15)
(1.15)
Аналогично можно получить формулу для вероятности суммы n совместных событий А1, А2, ... Аn.
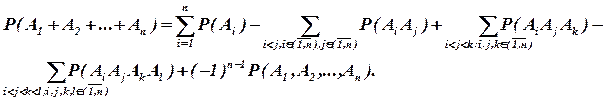 (1.16)
(1.16)
Дата добавления: 2016-12-09; просмотров: 2920;











