Основные теоретические сведения.

СЛУЧАЙНЫЕ события и их вероятности

Прежде чем рассматривать указанные подходы, определим единицу измерения вероятности события. В качестве такой единицы естественно взять вероятность достоверного события, т.е. такого, которое в результате опыта неизбежно должно произойти. Пример достоверного события – выпадение герба или решки при бросании монеты. Противоположностью достоверного события является невозможное событие – то, которое в данном опыте вообще не может произойти. Математики договорились приписать достоверному событию вероятность, равную единице, а невозможному – равную нулю. Все другие события "А" – возможные, но не достоверные будут характеризоваться вероятностями Р(А), лежащими между нулем и единицей. Таким об­разом, в общем случае вероятность Р(А) удовлетворяет условию: .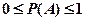

1.2. Непосредственный подсчет вероятностей (классическое опре­деление вероятности, математическая вероятность).

Существует класс опытов, для которых вероятности их возможных исходов (событий) можно вычислить, исходя непосредственно из самих условий опыта. Этих условий три.

1. Необходимо, чтобы различные исходы опыта – события были бы "объективно" одинаково возможными (равновозможными).

Пример – выпадение заданной грани симметричной игральной кос­ти "объективно" равновозможно.

2. События в данном опыте должны образовывать полную группу. Это означает, что в результате опыта неизбежно должно поя­виться хотя бы одно из событий группы.

Пример событий, образующих полную группу – выпадание 1, 2, 3, 4, 5, 6 очков при бросании игральной кости.

3. События в данном опыте должны быть несовместимы. Это означает, что в результате опыта никакие два события не могут появиться вместе.

Пример – при бросании игральной кости выпадает лишь одна грань.

События, которые удовлетворяют указанным условиям 1, 2, 3, называются случаями. Про такой опыт говорят, что он сводится к схеме случаев (к схеме урны).

Если опыт сводится к схеме случаев, то вероятность события А в данном опыте можно вычислить по соотношению:

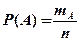, (1.1)

где 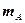- число случаев, благоприятных (соответствующих) событию А; 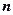- общее число случаев.

Пример 1.1. В полученной партии оказалось 200 ампул с новокаином, 100 ампул с лидокаином и 50 ампул с водой для инъекций. Наудачу вынимается одна из ампул. Чему равны вероятности получить ампулы с новокаином, с лидокаином и с водой для инъекций?

Решение. В нашем примере 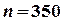, обозначим соответственно через А, В, С случайные события, состоящие, соответственно, в получении ампул с новокаином, с лидокаином и с водой для инъекций.

Легко видеть, что

Р(А) = 200:350; Р(В) = 100:350; Р(С) = 50:350.

Пример 1.2. Опыт состоит в одновременном (или последователь­ном) бросании двух монет. Найти вероятность события А = {хотя бы на одной монете выпадет герб}.

Решение. С первого взгляда может показаться, что в данной задаче три случая: A₁ - {два герба}; А₂ = {две решки}; А₃ ={герб и решка}. Однако есть сомнение, что эти события неравновозможны! Попытаемся составить для данного опыта схему случаев. Для этого назовем монеты первая и вторая, они вынимаются из урны и бросаются одновременно (или последовательно). Тогда можно назвать следующие случаи: В₁ = {на первой монете герб, на второй - герб}; В₂ ={на первой монете решка, на второй - решка}; В₃ = {на первой монете герб, на второй - решка}; В₄ = {на первой монете решка, на второй - герб).

Названные события В₁, В₂, В₃, В₄ можно считать равновероятными за счет перемешивания монет в урне в симметричности самих монет относительно герба и решки.

Найдем Р(А): n = 4; m_A = 3;Р(А) = 3:4.

Р(А₁) = 1:4;Р(А₂) = 1:4;Р(А₃) = 2:4.

Непосредственный подсчет вероятностей но формуле (1.1) может потребовать для вычисления чисел n и 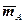использования комбинаторных формул числа перестановок, размещений, сочетаний:

Р_n = n! - число перестановок из n элементов;

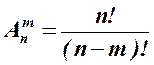- число размещений из n элементов по 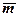(учитывается порядок расположения);

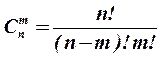- число сочетаний из n элементов по 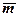(порядок расположения не учитывается).

Пример 1.3. В урне N перенумерованных шаров, k из них случайным образом по одному извлекаются и откладываются в сторону. Определить вероятность того, что номера последовательно извлекаемых шаров составят последовательность 1,2, ...., k (событие А).

Решение. Регламентируемый в условия случайный характер поочередного извлечения шаров позволяет допустить, что в результате рассматриваемого опыта любая последовательность k номеров из общего числа Nпоявляется с одинаковой возможностью. Этим опреде­лено "условие равновозможности" событий, образующих полную груп­пу и тем самым обосновано применение метода непосредственного под­счета вероятности события. Общее число равновозможных событий nравно числу различных групп по Кэлементов (номеров шаров) изобщего числа N , отличающихся как составом, так и порядком расположения элементов, т.е. числу размещений 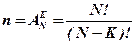. Число событий 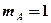(требуемая последовательность может появить­ся один раз):