Моделирование обеспечения деятельности строительного предприятия предметами труда

В любой задаче управления запасами требуется определить количество заказывае­мой продукции и сроки размещения заказов, которые можно удовлетворить путем создания запаса на весь период строительства или длякаждой единицы времени.

В первом случае тре­буются более высокие удельные (отнесенные к единице времени) капитальные вложения, но дефицит ресурсов возникает реже и частота размещения заказов меньше. Во втором случае наоборот удельные капитальные вложения снижаются, но частота размещения заказов и риск дефицита возрастают.

Размер и момент заказа определяют из условий минимизации суммарных затрат:

,

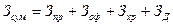где З_пр - затраты на приобретение;

З_оф - затраты на оформление;

З_хр - затраты на хранение;

З_д - потери (затраты) от дефицита.

Затраты на приобретение становятся важным фактором, когда цена единицы продукции зависит от размера заказа в виде оптовых скидок.

Затраты на оформление – представляют собой постоянные расходы, связанные с его размещением и при размещении более мелких заказов затраты возрастают.

Затраты на хранение – это расходы на содержание запаса на складе, которые возрастают с увеличением уровня запаса.

Потери от дефицита – расходы, обусловленные отсутствием запаса необходимой продукции.

Модель управления запасами не обязательно должна включать в себя все четыре вида затрат, так как некоторые из них могут быть незначительными. Большое разнообразие моделей этого класса и методов решения соответствующих задач во многом определя­ется характером спроса, который может быть детерминирован­ным (постоянным) или вероятностным.

Детерминированный спрос может быть статическим (интенсивность потребления остается неизменной во времени) или динамическим (спрос известен, но меняется во времени).

Вероятностный спрос может быть стацио­нарным (функция плотности вероятности спроса неизменна во времени) и нестационарным (функция плотности вероятности спроса изменяется во времени).

Кроме основного фактора – характера спроса влияние на выбор типа модели оказывают:

1. Запаздывания поставок или сроки выполнения заказов (детер­минированные или случайные).

2. Пополнение запаса (мгновенно от внешнего источника или равномерно во времени самой организа­цией).

Однопродуктовая статическая модель характеризуется постоянным во времени спросом, мгновенным пополнением запаса и отсутствием дефи­цита.

Интенсивность спроса в единицу времени равна 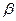. Наивысшего уровня запас достигает в момент поставки заказа размером Y (рис. 6.1). Уровень запаса достигает нуля спустя Y/β единиц времени после получения заказа размером Y. Продолжительность цикла движения заказа составляет t₀= Y/β, а средний уровень запаса равен Y/2.

Уровень запаса Y

Y/2

Время t

Рис. 6.1. Изменение уровня запаса (Y) во времени (t)

Величина Y выбирается из условия обеспечения сбалансированности между двумя видами затрат (частоты разрешения заказа и объема хранения запаса).

Суммарные затраты в единицу времени будут равны затратам на оформление заказа в единицу времени плюс затраты на хранение запасов в единицу времени:

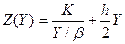, (6.2)

Экономичный размер заказа по формуле Чарли Уилсона имеет следующий вид:

,

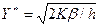где К - затраты на оформление заказа;

h - затраты на хра­нение единицы заказа в единицу времени;

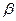- интенсивность спроса в единицу времени.

Оптимальная стратегия модели предусматривает заказ Y* единиц продукции каждые 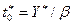единиц времени. Оптимальные затраты Z(Y*), получаемые путем непосредственной подстановки в формулу (7.2), составляют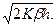

В точке Y* целевая функция Z(Y) при­нимает минимальное значение (рис. 6.2).

Пример 6.1. Ежедневный спрос на некоторый товар составляет около 100 ед. Затраты на размещение каждого запаса постоянны и равны 100 руб. Ежедневные затраты на хранение единицы запаса составляют 0,02 руб. Определить экономичный размер партии и точку заказа при сроке выполнения заказа, равном 12 дням.

Решение:

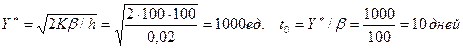
Так как срок выполнения заказа 12 дней, а продолжительность цикла составляет 10 дней, возобновление заказа происходит, когда уровень запаса достаточен для удовлетворения спроса на (12 - 10) = 2 дня. Таким образом, заказ размером 1000 ед. размещается, когда уровень запаса до­стигает 2 • 100 = 200 ед.

Для большинства реальных ситуаций существует срок выполнения заказа L от момента его размещения до действительной поставки. В практических ситуациях точку возобновления заказа определяют через уровень запаса, соответствующий моменту возобновления заказа.

Рис. 6.2.Определение точки

Y^* возобновления заказа через

уровень запаса:

А,Б. В, Г — точки возобновления

А Б В Г заказа

L₁ L₂ L₃ L₄ t

Пример 6.2. Строительная организация пополняет запас некоторого изделия, заказывая его в количестве достаточном для покрытия одноме­сячного спроса. Годовой спрос на изделие равен 1500 ед. Каждое разме­щение заказа оценивается затратами в 20 руб. Затраты на хранение одного изделия в течение месяца составляют 2 руб. Задолженность не допускается

Определить: оптимальный размер заказа, интервал времени между моментами размещения заказов и различие в годовых затратах при опти­мальной и применяемой стратегиях.

Решение. К= 20 руб., h = 2 руб.

При применяемой стратегии

β = 1500/12 = 125 ед./мес., Y= 1500/12 = 125 ед.

Z(Y) = K/(Y/β) + h(Y/2) = 20/(125/125) * 2(125/2) = 145 руб.

Тогда общие затраты за год составят 12 ۰ 145 = 1740 руб.

При оптимальной стратегии

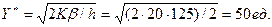
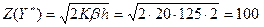руб.

Тогда общие затраты за год составят 12 * 100 = 1200 р.

Следовательно, различие в годовых затратах, руб.,

ΔZ = 1740 - 1200 = 540 руб.

Пример 6.3. Предположим теперь, что запас пополняется равномерно, а не мгновенно с интенсивностью α. Потребление равномерное с интенсивностью β в каждую единицу времени. Определим:

а) максимальный уровень запаса на складе;

б) общие затраты в единицу времени;

в) экономичный размер заказа.

Решение.

а) t₁ - Y/α - продолжительность поступления заказа;

(α - β) - интенсивность поступления заказа на склад.

Следовательно, Y/α (α - β) = Y(1 - β/α) - максимальный уровень запаса;

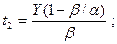
б) 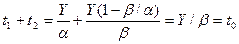— продолжительность цикла;

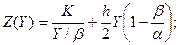
в) 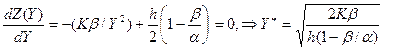(α > β )

На практике получил распространение приближенный метод, учитывающий вероятностный характер спроса. Создается некото­рый постоянный (буферный) запас на всем горизонте планиро­вания. Размер резерва В определяется таким образом, чтобы вероятность истощения запаса в течение периода L не превышала за­данной величины (рис. 6.3). Предположим, что ƒ(х) - плотность распределения вероятностей спроса в течение этого срока, а веро­ятность истощения запаса в течение периода L не должна превы­шать а.

Тогда размер резервного запаса B определяется из условия

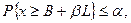
где βL - потребление в течение периода L.

B+Y^*

Рис. 6.3. Изменение запаса при

наличии резерва: B+βL А Б В

А, Б, В - точки возобновления заказа

B

L Время t

Предположим, что спрос в примере 6.1 в действительности представляет собой аппроксимацию случайной ситуация, при которой ежедневный спрос распределен нормально со средним математическим ожиданием µ =100 и средним квадратичным отклонением σ = 10. Определим размер резервного запаса таким образом, чтобы вероятность истощения запаса в течение срока выполнения заказа не превышала 0,05.

Решение.

Из примера 6.1 имеем L = 2 дня;

x_L=x₁+x₂, µ_L=µ₁+µ₂=100+100=200

Тогда дисперсия

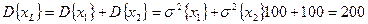
Таким образом, из формулы P{x_L ≥ B + βL} ≤ α, получаем

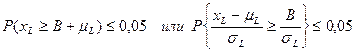Так как

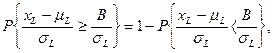то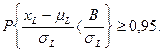

Теперь из таблицы для стандартного нормального распределе­ния получим —

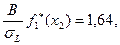т.е. В ≥ 14,14 х 1,64 = 23,2.

Однопродуктовая статическая модель с разрывами цен. Неред­ко цена единицы продукции зависит от размеров закупаемой партии. В таких случаях цены меняются скачкообразно. Предполо­жим, что цена единицы продукции равна с₁ при Y< q и с₂ при Y ≥ q, где с₁ > с₂, q — размер заказа, при превышении которого предоставляется скидка. В этом случае суммарные затраты за цикл должны также включать в себя издержки приобретения.

Суммарные затраты на единицу времени при Y< q

.

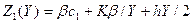При Y ≥ q эти затраты составляют

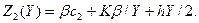
Графики этих функций приведены на рис 6.4.

Обозначим через Y_m — размер заказа, при котором достигается минимум функций Z₁ и Z₂. Тогда Y_m = 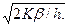Из вида функций Z₁ и Z₂ следует, что оптимальный размер заказа Y* зависит от того, где по отношению к зонам 1, 2, 3 находится точка разрыва цены q. Эти зоны находятся в результате определения q₁: (q₁ > Y_n) из уравнения Z₁(Y_m) = Z₂(q₁). Так как значение Y_m известно, то ре­шение уравнения дает значение величины q₁. Тогда зоны опреде­ляются следующим образом.

Зона 1: 0 < q < Y_m.

Зона 2: Y_m < q < q₁.

Зона 3: q> q_1.

Z Z₁ Z

Z₁

Z₂ Z₂

Зона 2 Z_m Зона 2

Зона 1 Зона 3 Зона 1 Зона 3

Y_m q₁ Y q Y_m q₁ Y

Рис. 6.4. Функции суммарных Рис. 6.5 Оптимальный размер

затрат на единицу времени заказа при нахождении точки

разрыва цены q в зоне 1

На рис. 6.5, 6.6, 6.7 приведено графическое решение задачи для различных случаев в зависимости от того, где находится q по отношению к зонам 1, 2, 3.

Z Z

Z₁ Z₁

Z₂ Z₂

Z_m

Z_m Зона 2 Зона 2

Зона 1 Зона 3 Зона 1 Зона 3

Y_m q q₁ Y Y_m q₁ q Y

Рис. 6.6. Оптимальный размер Рис. 6.7. Оптимальный размер заказа в зоне 2 заказа в зоне 3

Оптимальный размер заказа Y* определяется следующим образом:

Y_m, если 0 < q < Y_m (зона 1),

Y* = q, если Y_m < q < q₁ (зона 2),

Y_m , если q > q₁ (зона 3).

Пример 6.4. Рассмотрим модель управления запасами при следующих данных: К= 10 р., h = 1 р., р = 5 ед., с₁ = 2 р., с₂ = 1 p., q = 15 ед.

Решение. Вычислим размер заказа, при котором достигается минимум функций

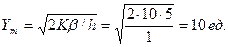
Так как q > Y_m , необходимо определить, где находится q: в зоне 2 или 3. Найдем значение q₁: Z₁ (Y_m) = Z₂ (q₁), следовательно, 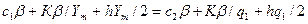или 2۰5 +10۰5/10+ 1۰10/2= 1۰5 +10۰5/q₁ + 1۰(q₁)/2, откуда q₁ = 26,18.

Так как Y_m < q < q₁, величина q находится в зоне 2. Таким образом, Y* = q= 15 ед. Суммарные затраты в единицу времени, руб.,

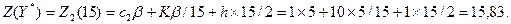
Однопродуктовая N-этапная динамическая модель. В этой моде­ли предполагается, что спрос известен, но может меняться от этапа к этапу. Пополнение запаса происходит мгновенно в начале этапа. Дефицит не допускается.

Построение динамической детерминированной модели сводится к исследованию конечного горизонта времени. Это не является серьезным ограничением, так как спрос в отдаленном будущем обычно не оказывает существенного влияния на решения, принимаемые для конечного горизонта времени. Кроме того, не име­ет смысла предполагать, что продукция будет храниться в запасе бесконечно.

Модель EOQ (Economic ordering quantity)основана на миними­зации совокупных затрат по закупке и хранению строительных материалов. Суммарные затраты предварительно подразделяются на две группы:

1. по закупке материалов (заказ, транспортировка, приемка то­варов, замена бракованного товара);

2. хранению материалов на складе или стройплощадке.

Сумма затрат по размещению заказов определяется по формуле:

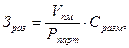
где V_п.м— объем производственного потребления материалов в рассматриваемом периоде;

Р_парт — средний размер поставки од­ной партии материалов;

С_разм — средняя стоимость размещения одного заказа.

Общая сумма затрат по размещению заказов снижается с рос­том среднего размера одной партии поставки материалов, при условии постоянного объема производственного потребления и средней стоимости размещения одного заказа.

С другой стороны, большой объем одной партии поставки ма­териалов вызывает рост затрат по хранению материалов на скла­де, так как при этом увеличивается время их хранения.

Формула для расчета затрат по хранению материалов на скла­де имеет следующий вид:

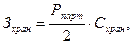
где С_хран — стоимость хранения единицы материалов в рассматри­ваемом периоде.

Общая сумма затрат по хранению материалов на складе снижается при уменьшении среднего размера одной партии поставки материалов и неизменной стоимости хранения единицы материалов в рассматриваемом периоде.

Модель EOQ позволяет оптимизировать соотношения между затратами по размещению заказа и хранению материалов на складе, чтобы их совокупная сумма была минимальной (рис. 7.8)

Сумма затрат

Точка EOQ Размер партии поставки

Рис. 6.8. Определение оптимального размера партии поставки материалов:

1 - минимальная сумма совокупных затрат; 2 — совокупная сумма затрат; 3 — сумма затрат по хранению материалов на складе; 4 — сумма затрат по размещению заказа

Математически модель EOQ может быть представлена следующей формулой:

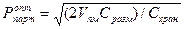
где 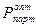- оптимальный средний размер партии поставки материалов (EOQ).

Оптимальный средний размер производственного запаса мате­риалов определяются по формуле

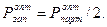
ПЛАНИРОВАНИЕ ОБЕСПЕЧЕНИЯ ДЕЯТЕЛЬНОСТИ СТРОИТЕЛЬНОГО ПРЕДПРИЯТИЯ СРЕДСТВАМИ ТРУДА

Планирование уровня механизации работ и потребности в строительных машинах и механизмах

Планирование механизации работ разрабатывается в строительно-монтажной организации для определения объема механизированных работ, потребности в машинах и механизмах и затрат на эксплуатацию.

При планировании механизации СМР предусматривается сокращение ручного труда на тяжелых и трудоемких процессах, происходит выбор наиболее эффективных машин для данных условий.

Исходные данные для разработки планов механизации следующие:

1. календарные планы движения строительных бригад;

2. ПОС и ППР;

3. отчетные и аналитические данные об использовании машин и оборудования;

4. данные о наличии и поступлении машин;

5. данные о планово-расчетных ценах 1 м/ч работ;

6. план технического развития и внедрения инноваций;

7. ведомости физических объемов работ по объектам и этапам работы;

8. договоры подряда и субподряда.

В процессе разработки плана механизации решаются следующие задачи:

1. расчет объема механизированных работ;

2. расчет уровня механизации, среднегодовой потребности в машинах, среднегодового количества машиносмен;

3. расчет стоимости эксплуатации машин и распределение по различным направлениям для отражения в смете затрат.

Уровень механизации позволяет дать количественную оценку (в %) и охарактеризовать структурные сдвиги в переходе от ручного труда к машинному:

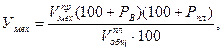(8.1)

где 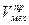— объем механизированных работ в предыдущем периоде;

Р_В — выполненный план повышения среднегодовой мощности парка машин %;

Р_пл — возможное (планируемое) повышение среднегодовой мощности парка машин;

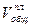— общий объем работ в планируемом году.

Среднегодовое число машиндля однородных работ:

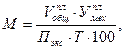(8.2)

где 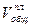— общий плановый объем работ;

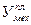— плановый пока­затель уровня механизации;

П_экс — часовая эксплуатационная про­изводительность машин;

Т — годовой фонд рабочего времени од­ной машины, ч.

Для машин, выполняющих разнородные работы, при которых не может быть установлен еди­ный измеритель производительности в натуральных единицах, нормы выработки устанавливают в часах.

При определении общего баланса потребности в машинах учитываются потребности в подсобном производстве, на погрузочно-разгрузочных работах и необходимость замены машин, выбывающих в планируемом году из-за физического и морального износа.

Количество машин, которое необходимо поставить на объекты в течение планируемого периода с учетом имеющихся на его начало, определяют, принимая во внимание сроки поставки инеобходимость замены машин, выбывающих в планируемом периоде вследствие физического и морального износа.

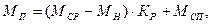
где М_ср— среднесписочное количество машин, требующихся на планируемый период;

М_н — количество машин данного вида на начало планируемого периода;

М_сп — количество машин списываемых в связи с физическим и моральным износом;

K_р — коэффи­циент равномерности, учитывающий равномерность поставки машин в планируемом периоде;

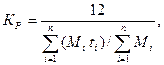
где М_i — число машин, поставляемых в партии;

t_i — срок работы этих машин до конца года;

ΣМ_i — число машин, поступивших в течение года.

Планирование использования парка строительных машин

Производительность одной машины, т.е. количество продукции или число операций, выполняемых ею за планируемый период, определяется плановой нормой выработки машины.

Плановые годовые нормы выработкиопределяются умножением плановых часовых норм на число часов работы соответствующих машин в год.

Плановая средняя часовая норма выработкирассчитывается по фактической производительности за предыдущий период и ее увеличению за счет осуществления ОТМ по плану технического развития.

Эта норма должна быть не ниже часовой эксплуатационной производительности аналогичных машин по ЕНиР с учетом поправочного коэффициента при переходе от выработки работа­ющих машин к выработке списочных машин. План нормы учитывает конкретные условия работы, использование опыта передовых строек, применяющих прогрессивные методы организации производства работ и эксплуатации строительных машин.

При планировании комплексной механизации норма выработки комплекса машин определяют по ведущей машине. Параметры остальных машин должны быть взаимоувязаны, чтобы обеспечивалась бесперебойная работа всего комплекса. Число часов, которые отрабатывает каждая среднесписочная машина, определяется по установленным годовым и сменным режимам ее работы.

Режим работыпредставляет собой распределение общего календарного времени на время работы машины, ее техническое обслуживание, ремонт, монтаж (демонтаж), перебазирование и простои по метеоусловиям.

Число смен работы основных строительных машин рассчитывается в годовом плане и должно быть не меньше двух. Число часов работы машины в смену предусматривается в годовом режиме и определяется на основе планового сменного режима работы, включающего в себя затраты времени на подготовительно-заключительные операции, технические и технологические перерывы.

Требуемые затраты времени на техническое обслуживание и ремонт рассчитывают исходя из плана технического обслужива­ния и ремонта и установленной продолжительности их выполне­ния. Затраты времени на перебазирование машин с объекта на объект, монтаж (демонтаж) определяют на основе рекомендаций НИИ или внутренних распоряжений.

Показатели использования машин в организации: