Влияние местных обратных связей на передаточные функции звеньев
Проблема обеспечения требуемых свойств линейных автоматических систем является весьма сложной. В ней могут быть выделены следующие частные задачи: обеспечение устойчивости (стабилизация) ; повышение запаса устойчивости (демпфирование) ; повышение точности регулирования в установившихся режимах (уменьшение или устранение статической ошибки воспроизведения задающего воздействия, уменьшение или устранение влияния постоянных возмущений) ; улучшение переходных процессов (увеличение быстродействия, максимальное уменьшение динамических ошибок воспроизведения воздействия и от возмущений) .
Иногда несколько частных задач могут быть решены совместно, в других случаях они оказываются противоречивыми. В зависимости от назначения системы и предъявляемых к ней требований одни задачи становятся основными, а другие отодвигаются на второй план или снимаются.
Всякая система автоматического регулирования должна быть устойчивой. Однако запас устойчивости в системе стабилизации (с постоянным или редко изменяемым задающим воздействием) может быть значительно меньше, чем в следящей системе (с непрерывно или часто изменяющимся задающим воздействием). Если параметры регулируемого объекта определены приближенно или могут изменяться в процессе эксплуатации системы, то необходим больший запас устойчивости, чем при точно установленных и неизменных параметрах.
В системах стабилизации обеспечивается максимально возможное или хотя бы необходимое уменьшение влияния возмущений. В следящих системах, кроме того, обеспечивается максимально возможное или необходимое быстродействие и уменьшение как статических, так и динамических ошибок воспроизведения задающего воздействия.
Требования в отношении быстродействия должны соответствовать мощности исполнительного элемента регулятора. Использование элементов для нужных преобразований сигнала управления не должно приводить к существенному повышению уровня помех, присутствующих в задающем воздействии.
Иногда устойчивость и необходимое качество регулирования удается достигнуть соответствующим выбором основных элементов регулятора - использованием менее инерционных устройств в качестве исполнительного элемента и усилителя.
Изменение динамических свойств основных элементов регулятора достигается также с помощью местных обратных связей. В отдельных случаях они могут быть созданы и внутри регулируемого объекта.
Влияние местных обратных связей весьма разнообразно. Предположим, что звено с передаточной функцией W охвачено отрицательной обратной связью с передаточной функцией W 0 . Тогда передаточная функция этого участка цепи W З =W/ (1+WW 0 ) .
Наиболее характерны следующие случаи. Пусть апериодическое звено охвачено жесткой обратной связью, т.е. W=k/ (Ts+1) и W 0 =K 0 . В этом случае
| W З =k/ (Ts+1+kk 0 ) =k З / (T З s+1) | (5.1) |
где k З =k/ (1+kk З ) и T З =T/ (1+kk 0 ) .
Таким образом, жесткая отрицательная обратная связь не изменяет структуру апериодического звена, но уменьшает его инерционность, т.е. уменьшает постоянную времени. Одновременно уменьшается передаточный коэффициент звена. Если обратная связь гибкая, т.е. W 0 =k 0 s , то
| W З =k/ (Ts+1+kk 0 s) =k З / (T З s+1) , | (5.2) |
где T З =T+kk 0
.
Следовательно, гибкая отрицательная обратная связь не изменяет структуру и не влияет на передаточный коэффициент апериодического звена. Она лишь увеличивает его инерционность - его постоянную времени.
Пусть интегрирующее звено охвачено жесткой обратной связью W=k/s и W 0 =k 0 .В этом случае
| W З =k/ (s+kk 0 ) =k З / (T З s+1) | (5.3) |
где k З =1/k 0 и T З =1/kk 0
.
Таким образом, жесткая отрицательная обратная связь превращает интегрирующее звено в апериодическое. Если обратная связь гибкая, т. е. W 0 =k 0 s , то
| W З =k/ (s+kk 0 s) =k З /s, | (5.4) |
где k З =k/ (1+kk 0 ) .
Гибкая обратная связь не изменяет структуру интегрирующего звена, но уменьшает его передаточный коэффициент (увеличивает постоянную времени интегрирования T З =1/k З ) .
Предположим, что колебательное звено охвачено жесткой обратной связью, т. е. W=k/ (T 2 s 2 + 2 x Ts+1) и W 0 =k 0 . При этом
| W З =k/ (T 2 s 2 +2 x Ts+1+kk 0 ) =k З / (T З 2 s 2 +2 x З T З s+1) , | (5.5) |
где
| k З =k/ (1+kk 0 ) , | 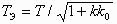 и и
| 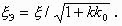
|
Жесткая отрицательная обратная связь не изменяет структуру колебательного звена, но уменьшает постоянную времени и коэффициент демпфирования. Уменьшается также передаточный коэффициент звена.
При гибкой обратной связи, т. е. W 0 =k 0 s , возможны два варианта. Если
| k 0 <2T (1- x ) /k | (5.6) |
то
| W З =k/ (T 2 s 2 +2 x Ts+1+kk 0 s ) =k/ (T 2 s 2 +2 x З T s+1) , | (5.7) |
где x З = x +kk 0 /2T. Слабая отрицательная гибкая связь не изменяет
структуру колебательного звена и лишь увеличивает его коэффициент демпфирования. Если же
| k 0 >2T (1- x ) /k, | (5.8) |
то
| W З =k/[ (T 1 s+1) (T 2 s+1) ], | (5.9) |
где 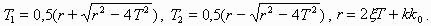
Сильная гибкая отрицательная обратная связь превращает колебательное звено в последовательное соединение двух апериодических звеньев.
Еще один случай; идеальное усилительное звено охвачено инерционной обратной связью, т. е. W=k и W 0 =k 0 / (T 0 s+1) . Тогда
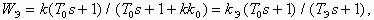
| (5.10) |
где k З =k/ (1+kk 0 ) и T З = T 0 / (1+kk 0 ) . Таким образом, инерционная отрицательная обратная связь превращает идеальное усилительное звено в реальное форсирующее, в звено, создающее производные от входного сигнала.
Из рассмотренных примеров можно заключить, что даже простейшие отрицательные обратные связи могут существенно изменить свойства типовых динамических звеньев. Еще больший эффект дают сложные отрицательные и положительные обратные связи. В [1, 3] подробно изложено влияние сложных обратных связей на свойства типовых динамических звеньев и их соединений.
Следовательно, если основные элементы регулятора по своей физической природе позволяют создать обратные связи, то динамические свойства этих элементов часто могут быть изменены в нужном направлении, в соответствии с поставленной целью.
Дата добавления: 2016-11-29; просмотров: 3043;











