РЕГУЛЯРНЫЙ РЕЖИМ ОХЛАЖДЕНИЯ (НАГРЕВА)

Анализ решений дифференциального уравнения теплопроводности

∂Т/ ∂t =αѲ Т (2.73)

показывает, что безразмерную избыточную температуру θ/θ_о можно выразить суммой произведений из трех величин:

_n=∞

θ/θ_о = ∑ A_nU_nexp(-m_nt), ( 2.74)

ⁿ⁼¹

где А_n - постоянные, зависящие от формы тела и начального

распределения температур;

U_n - функции координат, характеризующие изменение температуры в пространстве;

m_n – постоянные, представляющие собой ряд положительных возрастающих чисел

m₁ < m₂ <m₃ < ...< m_n. (2.75)

Такая форма записи безразмерной температуры пригодна не только для простейших тел правильной формы, но и для любых других тел, форма которых отражается на виде множителей А_n и U_n .

При небольшой продолжительности процесса теплообмена от t = 0 до t = t_р температурное поле определяется не только первым, но и последующими членами ряда. Температура в некоторых точках тела и скорость ее изменения зависят от начального распределения температур в теле. Это так называемая неупорядоченная стадия процесса охлаждения или нагревания.

Благодаря неравенству (2.75)сувеличением времени t ряд быстро сходится и все члены его, кроме первого, стремятся к нулю. При t, превышающем некоторое определенное значение t > t_р, начальные условия начинают играть второстепенную роль, и процесс полностью определяется только условиями охлаждения (нагревания) на поверхности тела, его физическими свойствами, геометрической формой и размерами. Вторая стадия охлаждения (нагревания) называетсярегулярным режимом и описывается первым членом ряда (индексы опущены):

θ/θ_о = АUexp(-mt), (2.76)

где m = μ₁²α /l² - темп регулярного режима.

Логарифмируя уравнение (2.76) , получим:

ln θ = - mt + С, (2.77)

где С = ln θ_оАU – функция от координат.

Из полученного уравнения видно, что регулярный режим теплопроводности характеризуется тем, что натуральный логарифм избыточной температуры θ = Т–Т_ж любой точки тела изменяется во времени по линейному закону, а начальное распределение температур в теле не оказывает влияния на форму этого уравнения. Это позволяет легко обнаружить в эксперименте наступление регулярного режима и, фиксируя температуру в произвольной точке тела для двух моментов времени t₁ и t₂, рассчитать темп охлаждения:

m = (ln θ₁ - ln θ₂) / (t₂ – t₁). (2.78)

На рис. 2.15 показано изменение температуры в двух точках тела при его охлаждении.

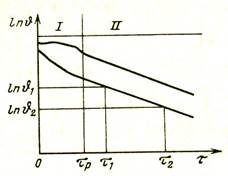
Рис. 2.15. Изменение во времени температуры тела

при его охлаждении: I – неупорядоченный процесс;

II – регулярный режим

Дифференцируя уравнение (2.77) по времени, получим

m = - (1/θ)(∂θ /∂t). (2.79)

Из этого уравнения следует, что темп регулярного режима охлаждения (нагревания) тела не зависит ни от координат, ни от времени и представляет собой относительную скорость изменения температуры. Он выражается в 1/с и в любой точке тела остается постоянным.

Темп регулярного режима определяется геометрической формой и размерами тела, его физическими свойствами и условиями теплообмена на поверхности тела (зависит от коэффициента теплоотдачи α).

Теория регулярного режима была разработана Г.М.Кондратьевым и применена им для определения теплофизических свойств тел (α, λ, с), коэффициента теплоотдачи α на поверхности тела, омываемого потоком жидкости, коэффициентов излучения.

Третья стадия охлаждения (нагревания) называетсястационарным режимом -приt → ∞ температура во всех точках тела становится равной температуре окружающей жидкости.

Контрольные вопросы

1. Приведите примеры нестационарной теплопроводности.
2. Опишите характер изменения температуры тела при его нагревании и охлаждении.
3. От каких параметров зависит температура любой точки тела при нестационарной теплопроводности.
4. Уравнение для безразмерной избыточной температуры тела.
5. Что представляют собой числа Био и Фурье?
6. Уравнение, описывающее нестационарное температурное поле в твердом теле.
7. Уравнения, описывающие изменение во времени безразмерной температуры для пластины и цилиндра.
8. Как пользоваться графиками для определения температуры тела при нестационарной теплопроводности.
9. Что называется регулярным режимом нагревания (охлаждения) тела.
10. По какой формуле рассчитывается темп охлаждения тела.