Общее уравнение плоскости
Поверхность и ее уравнение.
Поверхность в пространстве можно рассматривать как геометрическое место точек, удовлетворяющих какому-либо условию. Например, сфера радиуса 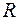 с центром в точке
с центром в точке 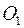 есть геометрическое место всех точек пространства, находящихся от точки
есть геометрическое место всех точек пространства, находящихся от точки 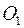 на расстоянии
на расстоянии 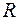 .
.
Уравнением данной поверхности в прямоугольной системе координат 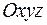 называется такое уравнение
называется такое уравнение 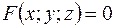 с тремя переменными х, у и z, которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности. Переменные х, у и z в уравнении поверхности называются текущими координатами точек поверхности.
с тремя переменными х, у и z, которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности. Переменные х, у и z в уравнении поверхности называются текущими координатами точек поверхности.
Уравнения плоскости в пространстве.
Простейшей поверхностью является плоскость. Плоскость в пространстве 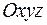 можно задать разными способами. Каждому из них соответствует определенный вид ее уравнения. Рассмотрим некоторые из них.
можно задать разными способами. Каждому из них соответствует определенный вид ее уравнения. Рассмотрим некоторые из них.
Общее уравнение плоскости
Общим уравнением плоскости называется уравнение первой степени с тремя переменными 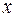 ,
, 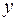 и
и 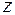 :
:
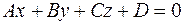 , (1)
, (1)
причем по крайней мере один из коэффициентов 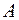 ,
, 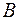 или
или 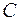 не равен нулю.
не равен нулю.
Вектор  называется нормальным вектором плоскости, он перпендикулярен плоскости (1).
называется нормальным вектором плоскости, он перпендикулярен плоскости (1).
Частные случаи общего уравнения плоскости:
1. Если 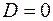 , то уравнение (1) принимает вид
, то уравнение (1) принимает вид
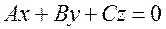 .
.
Этому уравнению удовлетворяет точка 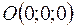 . Следовательно, в этом случае плоскость проходит через начало координат.
. Следовательно, в этом случае плоскость проходит через начало координат.
2. Если  , то имеем уравнение
, то имеем уравнение 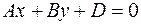 . Нормальный вектор
. Нормальный вектор 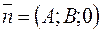 перпендикулярен оси
перпендикулярен оси  . Следовательно, плоскость параллельна оси
. Следовательно, плоскость параллельна оси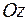 ; если В = 0 — плоскость параллельна оси
; если В = 0 — плоскость параллельна оси 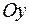 ,
, 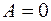 – параллельна оси
– параллельна оси 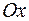 .
.
3. Если 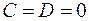 , то уравнение плоскости примет вид
, то уравнение плоскости примет вид 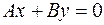 , в этом случае плоскость проходит через ось
, в этом случае плоскость проходит через ось 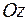 . Аналогично, уравнениям
. Аналогично, уравнениям 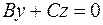 и
и 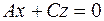 отвечают плоскости, проходящие соответственно через оси
отвечают плоскости, проходящие соответственно через оси 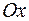 и
и 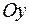 .
.
4. Если 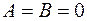 , то уравнение (1) принимает вид
, то уравнение (1) принимает вид 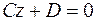 , т. е.
, т. е. 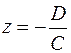 . Плоскость параллельна плоскости
. Плоскость параллельна плоскости  . Аналогично, уравнениям
. Аналогично, уравнениям 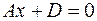 и
и 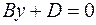 отвечают плоскости, соответственно параллельные плоскостям
отвечают плоскости, соответственно параллельные плоскостям 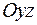 и
и 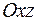 .
.
5. Если 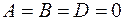 , то уравнение (1) примет вид
, то уравнение (1) примет вид 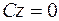 , т. е.
, т. е. 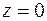 . Это уравнение плоскости
. Это уравнение плоскости  . Аналогично:
. Аналогично:  — уравнение плоскости
— уравнение плоскости 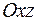 ;
;  — уравнение плоскости
— уравнение плоскости 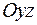 .
.
Дата добавления: 2016-11-29; просмотров: 1537;











