Уравнение прямой в пространстве, проходящей через две точки.

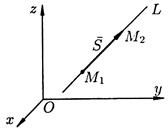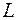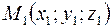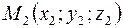Пусть прямая проходит через точки и . В качестве направ­ляющего вектора 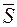можно взять вектор 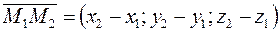, т. е. 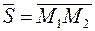(рис. 3). Следовательно, 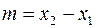, , 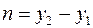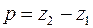. Поскольку прямая проходит через точ­ку 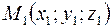, то, согласно уравнениям (11), уравнение прямой 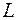имеет вид

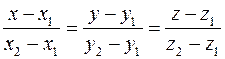. (12)

Уравнения (12) называются уравнениями прямой, проходящей через две данные точки.

Основные задачи, использующие уравнения прямой в пространстве.

Угол между прямыми. Условия параллельности и перпендикулярности прямых.

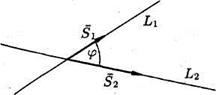
Пусть прямые 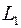и 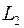заданы уравнениями

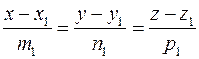
и .

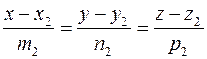Под углом между этими прямыми понимают угол между направляющими векторам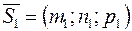и и 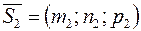(рис. 4). Поэтому, по извест­ной формуле для косинуса угла между векторами, получаем

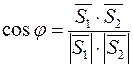, или

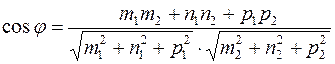. (13)

Для нахождения острого угла между прямым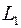и и 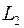числитель правой части формулы (13) следует взять по модулю.

Если прямые 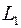и 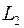перпендикулярны, то в этом и только в этом случае имеем 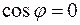. Следовательно, числитель дроби (13) равен нулю, т. е. .

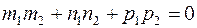Если прямые 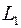и 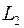параллельны, то параллельны их направляющие векторы 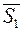и 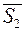. Следовательно, координаты этих векторов пропорциональны, т. е. .

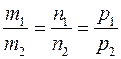Взаимное расположение прямой и плоскости в пространстве.